
分析 先利用函数的周期性、奇偶性,把自变量转化到所给的区间[0,1],即可求出函数值.
解答 解:∵函数f(x)最小正周期为2,∴f($\frac{13}{4}$)=f($\frac{13}{4}$-4)=f(-$\frac{3}{4}$),
又∵函数f(x)是定义在R上的奇函数,∴f(-$\frac{3}{4}$)=-f($\frac{3}{4}$),
∵当0≤x≤1时,f(x)=log2(4x+1),
∴f($\frac{3}{4}$)=log2(4×$\frac{3}{4}$+1)=log24=2,
∴f($\frac{13}{4}$)=-f($\frac{3}{4}$)=-2.
故答案为:-2.
点评 本题综合考查了函数的奇偶性、周期性及函数值,充分理解以上有关知识是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 135° | D. | -45° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
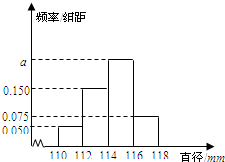 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品A中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品A中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a6>b6 | B. | a6=b6 | C. | a6<b6 | D. | a6>b6或a6<b6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,8) | B. | {3,5,7} | C. | {0,1,3,5,7} | D. | {1,3,5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com