
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
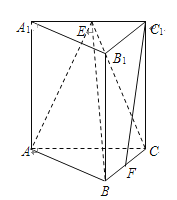
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)先利用线面垂直得到线线垂直,再利用线面垂直的判定定理和面面垂直的判定定理进行证明;(2)利用三角形的中位线得到线线平行和线段,得到平行四边形,再由平行四边形的性质得到线线平行,再由线面平行的判定定理进行证明;(3)利用三棱锥的体积公式进行求解.
试题解析:(Ⅰ)证明:在三棱柱![]() 中,
中,
![]() 底面
底面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()
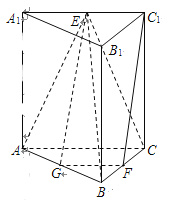
(Ⅱ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
因为![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,![]() .
.
因为![]() ,且
,且![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅲ)因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
所以三棱锥![]() 的体积
的体积
![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上除顶点外的任意点,直线
上除顶点外的任意点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
, ![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数t满足f(0)=f(2)=2,f(1)=1.
(1)求函数f(x)的解析式;
(2)当x∈[﹣1,2]时,求y=f(x)的值域;
(3)设h(x)=f(x)﹣mx在[1,3]上是单调函数,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
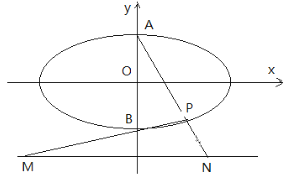
【题目】如图椭圆![]() 的上下顶点为A、B,直线
的上下顶点为A、B,直线![]() :
: ![]() ,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线
,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线![]() 于点N,连结BP并延长交直线
于点N,连结BP并延长交直线![]() 于点M,设AP、BP所在直线的斜率分别为
于点M,设AP、BP所在直线的斜率分别为![]() ,若椭圆的离心率为
,若椭圆的离心率为![]() ,且过点
,且过点![]() ,(1)求
,(1)求![]() 的值,并求
的值,并求![]() 最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com