
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分6分.
已知点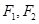 为双曲线
为双曲线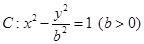 的左、右焦点,过
的左、右焦点,过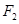 作垂直于
作垂直于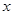 轴的直线,在
轴的直线,在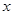 轴上方交双曲线于点
轴上方交双曲线于点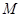 ,且
,且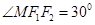 ,圆
,圆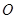 的方程为
的方程为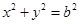 .
.
(1)求双曲线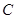 的方程;
的方程;
(2)过圆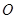 上任意一点
上任意一点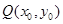 作切线
作切线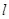 交双曲线
交双曲线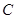 于
于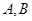 两个不同点,
两个不同点,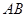 中点为
中点为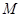 ,
,
求证: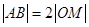 ;
;
(3)过双曲线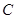 上一点
上一点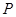 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是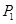 和
和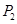 ,求
,求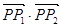 的值
的值
(1) ;(2)见解析;(3)
;(2)见解析;(3)
【解析】本试题主要考查了双曲线的运用。
解:(1)设 的坐标分别为
的坐标分别为 ----------------1分
----------------1分
因为点M在双曲线C上,所以 ,即
,即 ,所以
,所以 ------2分
------2分
在
 中,
中, ,
, ,所以
,所以 -------3分
-------3分
由双曲线的定义可知:
故双曲线C的方程为: -------------------4分
-------------------4分
(2)①当切线l的斜率存在
设 ,切线
,切线 的方程为:
的方程为: 
代入双曲线C中,化简得:
所以 -------------------6分
-------------------6分
因为直线l与圆O相切,所以 ,代入上式,得
,代入上式,得 -----------7分
-----------7分
设点M的坐标为 ,则
,则

所以-------------------8分
即|AB|=2|OM|成立
②当切线l的斜率不存在时,
 ,
,
即|AB|=2|OM|成立-------------------10分
(1) 由条件可知:两条渐近线分别为

 ------11分
------11分
设双曲线C上的点P(x0,y0),
则点P到两条渐近线的距离分别为 --------------13分
--------------13分
因为P(x0,y0),在双曲线C: 上,所以
上,所以
故 -------------------14分
-------------------14分
设 -------------15分
-------------15分
-----16分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011-2012学年上海市徐汇区高三4月学习能力诊断理科数学试卷(解析版) 题型:解答题
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数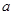 使得数列
使得数列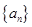 满足:若
满足:若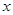 是数列
是数列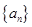 中的一项,则
中的一项,则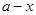 也是数列
也是数列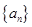 中的一项,称数列
中的一项,称数列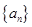 为“兑换数列”,常数
为“兑换数列”,常数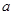 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: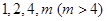 是“兑换系数”为
是“兑换系数”为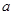 的“兑换数列”,求
的“兑换数列”,求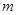 和
和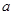 的值;
的值;
(2)已知有穷等差数列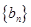 的项数是
的项数是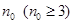 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列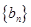 是“兑换数列”,并用
是“兑换数列”,并用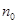 和
和 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列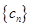 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市徐汇区高三4月学习能力诊断理科数学试卷(解析版) 题型:解答题
第(1)小题满分4分,第(2)小题满分8分.
在 中,角
中,角 所对边的长分别为
所对边的长分别为 ,且
,且 .
.
(1)求 的值;(2)求
的值;(2)求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分)第(1)小题满分4分,第(2)小题满分8分,第(3)小题满分6分。
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆![]() 。
。
若椭圆![]() ,判断
,判断![]() 与
与![]() 是否相似?如果相似,求出
是否相似?如果相似,求出![]() 与
与![]() 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
 写出与椭圆
写出与椭圆![]() 相似且短半轴长为
相似且短半轴长为![]() 的椭圆
的椭圆![]() 的方程;若在椭圆
的方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围?
的取值范围?
如图:直线![]() 与两个“相似椭圆”
与两个“相似椭圆”![]() 和
和![]() 分别交于点
分别交于点![]() 和点
和点![]() ,证明:
,证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)第(1)小题满分4分,第(2)小题满分8分。
已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() 。
。
(1)若![]() ,求
,求![]() ;(2)若
;(2)若![]() ,求正数
,求正数![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com