
【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: ①﹣3是函数y=f(x)的极值点;
②﹣1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(﹣3,1)上单调递增.
则正确命题的序号是 . 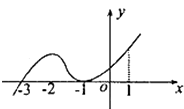
【答案】①④
【解析】解:根据导函数图象可知当x∈(﹣∞,﹣3)时,f'(x)<0,在x∈(﹣3,1)时,f'(x)≤0 ∴函数y=f(x)在(﹣∞,﹣3)上单调递减,在(﹣3,1)上单调递增,故④正确
则﹣3是函数y=f(x)的极小值点,故①正确
∵在(﹣3,1)上单调递增∴﹣1不是函数y=f(x)的最小值点,故②不正确;
∵函数y=f(x)在x=0处的导数大于0∴切线的斜率大于零,故③不正确
所以答案是:①④
【考点精析】掌握利用导数研究函数的单调性和函数的极值是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;极值反映的是函数在某一点附近的大小情况.
在这个区间单调递减;极值反映的是函数在某一点附近的大小情况.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】已知a、b、c分别是△ABC的三个内角A、B、C的对边.
(1)若△ABC面积S△ABC= ![]() ,c=2,A=60°,求a、b的值;
,c=2,A=60°,求a、b的值;
(2)若a=ccosB,且b=csinA,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a1=2,前n项和为Sn , 若数列{an+1}也是等比数列,则Sn等于( ).
A.2n+1-2
B.3n
C.2n
D.3n-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,右焦点为(
,右焦点为( ![]() ,0)
,0)
(1)求椭圆C的方程;
(2)若过原点 ![]() 作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体 ![]() 中,
中, ![]() 分别为
分别为 ![]() 的中点.
的中点.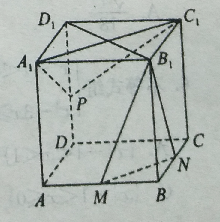
(1)求证:平面 ![]() ⊥平面
⊥平面 ![]() ;
;
(2)当点 ![]() 在
在 ![]() 上运动时,是否都有
上运动时,是否都有 ![]() 平面
平面 ![]() ,证明你的结论;
,证明你的结论;
(3)若 ![]() 是
是 ![]() 的中点,试判断
的中点,试判断 ![]() 与平面
与平面 ![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(x0 , y0)在x2+y2=r2(r>0)外,则直线x0x+y0y=r2与圆x2+y2=r2的位置关系为( )
A.相交
B.相切
C.相离
D.相交、相切、相离三种情况均有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com