已知直线3x+4y-2=0与直线2x-3y+10=0的交点为P,
(1)求经过点P且垂直于直线3x-2y+4=0的直线方程;
(2)求圆心在y轴且经过点P和原点的圆的方程.
【答案】
分析:(1)解方程组求得点P的坐标,根据两条直线垂直的性质设出所求的直线方程为2x+3y+c=0,把把点P的坐标代入求得c的值,可得所求的直线方程.
(2)设圆心的坐标为(0,b),则由圆经过点P和原点可得 0+b
2=(0+2)
2+(b-2)
2,求得b的值,可得圆心和半径,从而求得所求圆的方程.
解答:解:(1)由
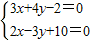
求得
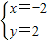
,故点P(-2,2).
设经过点P且垂直于直线3x-2y+4=0的直线方程为2x+3y+c=0,把点P的坐标代入求得c=-2,故所求的直线方程为 2x+3y-2=0.
(2)设圆心的坐标为(0,b),则由圆经过点P和原点可得 0+b
2=(0+2)
2+(b-2)
2,求得b=2,故半径为
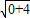
=2,
故所求的圆的方程为 x
2+(y-2)
2=4.
点评:本题主要考查求两条直线的交点坐标,两条直线垂直的性质,用待定系数法求直线方程,求圆的标准方程,属于中档题.

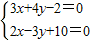 求得
求得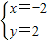 ,故点P(-2,2).
,故点P(-2,2).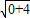 =2,
=2,

 名校课堂系列答案
名校课堂系列答案