
【题目】如图,三棱锥D-ABC中,![]()
![]()
![]() ,E,F分别为DB,AB的中点,且
,E,F分别为DB,AB的中点,且![]() .
.
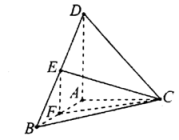
(1)求证:平面![]() 平面ABC;
平面ABC;
(2)求二面角D-CE-F的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,可得
,可得![]() ,
,![]() ,从而得到
,从而得到![]() 平面
平面![]() ,得到
,得到![]() ,由
,由![]() ,
,![]() ,得到
,得到![]() ,从而得到
,从而得到![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,建立空间直角坐标系,利用余弦定理和勾股定理,得到
为原点,建立空间直角坐标系,利用余弦定理和勾股定理,得到![]() ,
,![]() ,得到
,得到![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,根据向量夹角的余弦公式,得到二面角
,根据向量夹角的余弦公式,得到二面角![]() 的余弦值
的余弦值
(1)如图取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
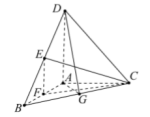
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
所以![]() .
.
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,即
,即![]() ,
,
则![]() .
.
又因为![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面DAB,
平面DAB,
所以平面![]() 平面
平面![]() .
.
(2)因为![]() 平面
平面![]() ,则以
,则以![]() 为坐标原点,
为坐标原点,
过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴,![]() 为
为![]() 轴,AD为
轴,AD为![]() 轴,
轴,
建立如下图所示的空间直角坐标系.
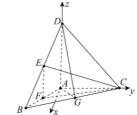
因为![]()
![]()
![]() ,
,
在![]() 中,
中,
![]()
![]()
![]() ,
,
所以![]() .
.
在![]() 中,
中,![]()
![]() ,
,
所以点![]() ,
,![]()
![]()
![]() ,
,

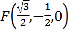 .
.
设平面![]() 的法向量为
的法向量为![]()
![]()
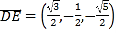 .
.
所以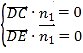 ,即
,即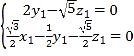 ,
,
可取![]() .
.
设平面![]() 的法向量为
的法向量为![]()
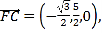
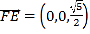 .
.
所以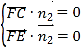 ,即
,即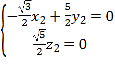 ,
,
可取![]() ,
,
则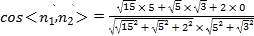
![]()
因为二面角![]() 为钝二面角,所以二面角
为钝二面角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程数”,收集了使用该型号电动汽车![]() 年以上的部分客户的相关数据,得到他们的电动汽车的“实际平均续航里程数”.从年龄在40岁以下的客户中抽取10位归为A组,从年龄在40岁(含40岁)以上的客户中抽取10位归为B组,将他们的电动汽车的“实际平均续航里程数”整理成下图,其中“+”表示A组的客户,“⊙”表示B组的客户.
年以上的部分客户的相关数据,得到他们的电动汽车的“实际平均续航里程数”.从年龄在40岁以下的客户中抽取10位归为A组,从年龄在40岁(含40岁)以上的客户中抽取10位归为B组,将他们的电动汽车的“实际平均续航里程数”整理成下图,其中“+”表示A组的客户,“⊙”表示B组的客户.
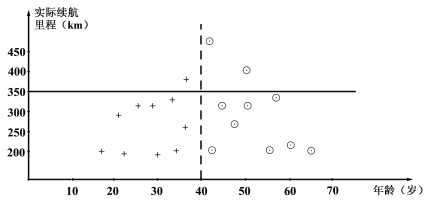
注:“实际平均续航里程数”是指电动汽车的行驶总里程与充电次数的比值.
(Ⅰ)记A,B两组客户的电动汽车的“实际平均续航里程数”的平均值分别为![]() ,
,![]() ,根据图中数据,试比较
,根据图中数据,试比较![]() ,
,![]() 的大小(结论不要求证明);
的大小(结论不要求证明);
(Ⅱ)从A,B两组客户中随机抽取2位,求其中至少有一位是A组的客户的概率;
(III)如果客户的电动汽车的“实际平均续航里程数”不小于350,那么称该客户为“驾驶达人”.从A,B两组客户中,各随机抽取1位,记“驾驶达人”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (
(![]() ,
,![]() )的一条渐近线方程为
)的一条渐近线方程为![]() ,点
,点![]() 在双曲线上;抛物线
在双曲线上;抛物线![]() (
(![]() )的焦点F与双曲线的右焦点重合.
)的焦点F与双曲线的右焦点重合.
(1)求双曲线和抛物线的标准方程;
(2)过焦点F作一条直线l交抛物线于A,B两点,当直线l的斜率为![]() 时,求线段
时,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受电视机在保修期内维修费等因素的影响,企业生产每台电视机的利润与该电视机首次出现故障的时间有关.某电视机制造厂生产甲、乙两种型号电视机,保修期均为2年,现从该厂已售出的两种型号电视机中各随机抽取50台,统计数据如下:
品牌 | 甲 | 乙 | |||
首次出现故障时间x(年) |
|
|
|
|
|
电视机数量(台) | 3 | 5 | 42 | 8 | 42 |
每台利润(千元) | 1 | 2 | 3 | 1.8 | 2.8 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲种型号电视机中随机抽取一台,求首次出现故障发生在保修期内的概率;
(2)该厂预计今后这两种型号电视机销量相当,由于资金限制,只能生产其中一种型号电视机,若从经济效益的角度考虑,你认为应该产生哪种型号电视机?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关,现收集了该种药用昆虫的6组观测数据如下表:
温度x/℃ | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得:
![]() ,
,![]() ,
,![]() 线性回归模型的残差平方和
线性回归模型的残差平方和![]() ,
,![]() ,
,
其中![]() 分别为观测数据中的温度和产卵数,
分别为观测数据中的温度和产卵数,![]()
(1)若用线性回归模型,求y关于x的回归方程![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求得y关于x的回归方程为![]() ,且相关指数
,且相关指数![]() .
.
①试与1中的回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为35℃时该用哪种药用昆虫的产卵数(结果取整数)
附:一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为 ,
,![]() ;相关指数
;相关指数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
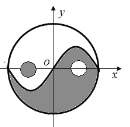
【题目】太极是中国古代的哲学术语,意为派生万物的本源.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼.太极图形象化地表达了阴阳轮转,相反相成是万物生成变化根源的哲理.太极图形展现了一种互相转化,相对统一的形式美.按照太极图的构图方法,在平面直角坐标系中,圆![]() 被
被![]() 的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为
的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为![]() ,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com