
【题目】已知向量 ![]() =(2cos2x,
=(2cos2x, ![]() ),
), ![]() =(1,sin2x),函数f(x)=
=(1,sin2x),函数f(x)= ![]()
![]() ﹣1.
﹣1.
(1)当x= ![]() 时,求|a﹣b|的值;
时,求|a﹣b|的值;
(2)求函数f(x)的最小正周期以及单调递增区间;
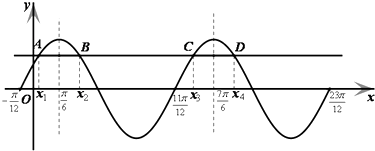
(3)求方程f(x)=k,(0<k<2),在[﹣ ![]() ,
, ![]() ]内的所有实数根之和.
]内的所有实数根之和.
【答案】
(1)
解:由向量 ![]() =(2cos2x,
=(2cos2x, ![]() ),
), ![]() =(1,sin2x),
=(1,sin2x),
则:a﹣b=(2cos2x﹣1, ![]() sin2x)
sin2x)
当x= ![]() 时,a﹣b=(2cos2
时,a﹣b=(2cos2 ![]() ﹣1,
﹣1, ![]() sin2×
sin2× ![]() )
)
=(0, ![]() )
)
那么:|a﹣b|= ![]()
(2)
解:f(x)=ab﹣1=1×2cos2x+ ![]() sin2x
sin2x
= ![]()
=1+cos2x+ ![]() sin2x﹣1
sin2x﹣1
=2sin(2x+ ![]() )
)
∴最小正周期T= ![]()
由sinx的图象和性质,可知x ![]() ,(k∈Z)是增区间.
,(k∈Z)是增区间.
∴2x+ ![]()
![]() 是增区间,即:
是增区间,即: ![]() ,(k∈Z)
,(k∈Z)
解得: ![]() ,(k∈Z)
,(k∈Z)
所以,f(x)的单调增区间为: ![]() ,(k∈Z)
,(k∈Z)
(3)
解:由方程f(x)=k,(0<k<2),得 ![]() .
.
∵ ![]() 的周期T=π,又
的周期T=π,又 ![]() ,
,
∴ ![]() 在
在 ![]() 内有2个周期.
内有2个周期.
∵ ![]() ,∴方程
,∴方程 ![]() 在
在 ![]() 内有4个交点,即有4个实根.
内有4个交点,即有4个实根.
根据图象的对称性,有 ![]() ,
, ![]() ,
,
∴所有实数根之和=x1+x2+x3+x4+x5+x6= ![]() .
.
【解析】(1)根据平面向量加减的运算法则求出a﹣b,化简,将x= ![]() 带入,求模长.(2)根据平面向量乘积的运算法则求出f(x),将其化简,结合三角函数的图象和性质即可得到答案.(3)利用三角函数的图象和性质,在[﹣
带入,求模长.(2)根据平面向量乘积的运算法则求出f(x),将其化简,结合三角函数的图象和性质即可得到答案.(3)利用三角函数的图象和性质,在[﹣ ![]() ,
, ![]() ]内求出方程f(x)=k时,x的值,即可解决问题.
]内求出方程f(x)=k时,x的值,即可解决问题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】王府井百货分店今年春节期间,消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对春节前7天参加抽奖活动的人数进行统计, ![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断变量![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该活动只持续10天,估计共有多少名顾客参加抽奖.
参与公式:  ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:若0<a<1,则不等式ax2﹣2ax+1>0在R上恒成立,命题q:a≥1是函数 ![]() 在(0,+∞)上单调递增的充要条件;在命题 ①“p且q”、②“p或q”、③“非p”、④“非q”中,假命题是 .
在(0,+∞)上单调递增的充要条件;在命题 ①“p且q”、②“p或q”、③“非p”、④“非q”中,假命题是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的最小正周期为π,若其图象向左平移
的最小正周期为π,若其图象向左平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于点 ![]() 对称
对称
C.关于直线 ![]() 对称
对称
D.关于直线 ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且
上,且![]() .
.

(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的二面角的正弦值及四棱锥
所成的二面角的正弦值及四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣6x﹣8y﹣5t=0,直线l:x+3y+15=0.
(1)若直线l被圆C截得的弦长为 ![]() ,求实数t的值;
,求实数t的值;
(2)当t=1时,由直线l上的动点P引圆C的两条切线,若切点分别为A,B,则在直线AB上是否存在一个定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,
PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求三棱锥Q-ACD的体积。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com