
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() ﹣ax(a∈R).
﹣ax(a∈R).
(1)当a= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)若函数f(x)在[﹣1,1]上为单调函数,求实数a的取值范围.
【答案】
(1)解:当a= ![]() 时,函数f(x)=
时,函数f(x)= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() x,
x,
∴f′(x)= ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() ,
,
令f′(x)=0,解得x=0.或x=ln2,
当f′(x)>0时,即x<0,或x>ln2,故函数f(x)单调递增,
当f′(x)<0时,即0<x<ln2,故函数f(x)单调递减,
所以函数f(x)单调增区间为(﹣∞.0)∪(ln2,+∞),单调减区间为(0,ln2)
(2)解:∵f′(x)= ![]() +
+ ![]() ﹣a,
﹣a,
①若函数f(x)在[﹣1,1]上为单调减函数,
∴f′(x)= ![]() +
+ ![]() ﹣a≤0,在[﹣1,1]恒成立,
﹣a≤0,在[﹣1,1]恒成立,
即a≥ ![]() +
+ ![]()
令g(x)= ![]() +
+ ![]() ,
,
则g′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
当x∈[﹣1,ln ![]() ),g(x)单调递减,x∈(ln
),g(x)单调递减,x∈(ln ![]() ,1]单调递增,
,1]单调递增,
又因为g(1)= ![]() ,g(﹣1)=
,g(﹣1)= ![]() ,
,
g(1)<g(﹣1),
故g(x)max=g(﹣1)= ![]() ,
,
![]() ,
,
②若函数f(x)在[﹣1,1]上为单调增函数,
∴f′(x)= ![]() +
+ ![]() ﹣a>0,在[﹣1,1]恒成立,
﹣a>0,在[﹣1,1]恒成立,
即a< ![]() +
+ ![]()
令h(x)= ![]() +
+ ![]() ,
,
则h′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
当x∈[﹣1,ln ![]() ),g(x)单调递减,x∈(ln
),g(x)单调递减,x∈(ln ![]() ,1]单调递增,
,1]单调递增,
故当x=ln ![]() ,h(x)有最小值,最小值为h(x)min=h(ln
,h(x)有最小值,最小值为h(x)min=h(ln ![]() )=
)= ![]()
故a≤ ![]() ,
,
综上所述实数a的取值范围为(﹣∞, ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
【解析】(1)先求导,再根据导数求出函数的单调区间;(2)需要分两类,函数f(x)在[﹣1,1]上为单调减函数和函数f(x)在[﹣1,1]上为单调增函数,然后分离参数,根据函数的最值,求出范围即可.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣2sin2x+2 ![]() sinxcosx+1.
sinxcosx+1.
(1)求f(x)的最小正周期及对称中心;
(2)若x∈[﹣ ![]() ,
, ![]() ],求f(x)的最大值和最小值.
],求f(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
请回答:
(Ⅰ)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(Ⅱ)根据1的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为 ,
,![]() ,
,
相关系数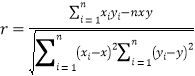 .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( )
①对于命题p:x∈R,使得x2+x﹣1<0,则¬p:x∈R,均有x2+x﹣1>0;
②p是q的必要不充分条件,则¬p是¬q的充分不必要条件;
③命题“若x=y,则sinx=siny”的逆否命题为真命题;
④“m=﹣1”是“直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直”的充要条件.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com