
 ,①当这3人之间比赛0场时,由于
,①当这3人之间比赛0场时,由于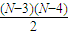 +6=50,N无整数解,
+6=50,N无整数解,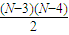 +5=50,解得N=13,满足条件.③当这3人之间比赛2场时,由于
+5=50,解得N=13,满足条件.③当这3人之间比赛2场时,由于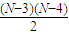 +4=50,N无整数解,故舍去,从而得到结论.
+4=50,N无整数解,故舍去,从而得到结论. =
=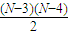 .
. +6=50,N无整数解,故舍去.
+6=50,N无整数解,故舍去.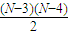 +5=50,N=13,是整数解,满足条件.
+5=50,N=13,是整数解,满足条件.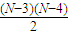 +4=50,N无整数解,故舍去.
+4=50,N无整数解,故舍去.

 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:2010年广西贵港市、柳州市、钦州市4月高考数学模拟试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com