②③④
分析:①利用诱导公式可将y=sin
4x-cos
4x化为y=-cos2x,可求出其周期,从而可判断出①的真假.
②在△ABC中,由A>B,可得到

,
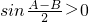
,再化sinA-sinB=

,故可判断出②真假.
③利用诱导公式得sinβ=cos(
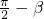
),再利用余弦函数y=cosx在区间[0,

]上单调递减,即可判断出③的真假.
④利用平移变换的法则“对自变量x左加右减”可得平移后的表达式,进而可判断出.
⑤由已知0<x<π,可得

,进而可判断出y=sin(x-

)在区间(0,π)上的单调性,可判断出⑤的真假.
解答:①∵y=sin
4x-cos
4x=(sin
2x-cos
2x)(sin
2x+cos
2x)=-cos2x,∴T=

=π.∴函数y=sin
4x-cos
4x的最小正周期是 π.故①假命题.
②在△ABC中,∵0<B<A<π,∴0<A+B<π,0<A-B<π,∴0<

<

,0

,∴
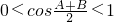
,
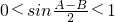
,
∴sinA-sinB=

>0,∴sinA>sinB.故②正确.
③∵cosα>sinβ,∴cosα>cos(
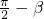
),∵α、β是锐角,∴
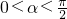
,
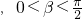
,∴

,
又∵y=cosx在区间[0,

]上单调递减,∴

,∴
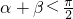
,故③正确.
④把函数y=3sin(2x+

)的图象向右平移

得到 y=3sin[2
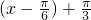
]=3sin2x的图象,故④正确.
⑤∵0<x<π,∴

,∴y=sin(x-

)在区间(0,π)上单调递增,故⑤是假命题.
综上可知:正确命题的序号是②③④.
故答案是②③④.
点评:本题综合考查了三角函数的图象与性质,熟练掌握三角函数的图象与性质是正确做好本题的关键.

 ;
; )的图象向右平移
)的图象向右平移 得到y=3sin2x的图象;
得到y=3sin2x的图象; )在(0,π)上是减函数
)在(0,π)上是减函数 ,
,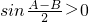 ,再化sinA-sinB=
,再化sinA-sinB= ,故可判断出②真假.
,故可判断出②真假.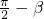 ),再利用余弦函数y=cosx在区间[0,
),再利用余弦函数y=cosx在区间[0, ]上单调递减,即可判断出③的真假.
]上单调递减,即可判断出③的真假. ,进而可判断出y=sin(x-
,进而可判断出y=sin(x- )在区间(0,π)上的单调性,可判断出⑤的真假.
)在区间(0,π)上的单调性,可判断出⑤的真假. =π.∴函数y=sin4x-cos4x的最小正周期是 π.故①假命题.
=π.∴函数y=sin4x-cos4x的最小正周期是 π.故①假命题. <
< ,0
,0 ,∴
,∴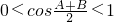 ,
,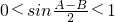 ,
, >0,∴sinA>sinB.故②正确.
>0,∴sinA>sinB.故②正确.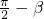 ),∵α、β是锐角,∴
),∵α、β是锐角,∴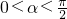 ,
,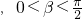 ,∴
,∴ ,
, ]上单调递减,∴
]上单调递减,∴ ,∴
,∴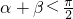 ,故③正确.
,故③正确. )的图象向右平移
)的图象向右平移 得到 y=3sin[2
得到 y=3sin[2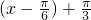 ]=3sin2x的图象,故④正确.
]=3sin2x的图象,故④正确. ,∴y=sin(x-
,∴y=sin(x- )在区间(0,π)上单调递增,故⑤是假命题.
)在区间(0,π)上单调递增,故⑤是假命题.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案