
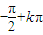 ,
,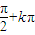 )(k∈Z),但在R上不是增函数,如α=
)(k∈Z),但在R上不是增函数,如α=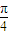 和β=
和β=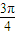 的正切值之间的关系,故①错,
的正切值之间的关系,故①错,

 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
①作正弦函数图象时,单位圆的半径长与x轴的单位长度可以不一致 ②y=sinx,x∈[0,2π]的图象关于点P(π,0)成中心对称图形 ③y=cosx,x∈[0,2π]的图象关于x=π成轴对称图形 ④正、余弦函数y=sinx,y=cosx的图象不超出y=-1与y=1所夹的区域
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省济宁市微山一中高一(下)期末数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com