试题分析:(1) 首先应用待定系数法根据已知图形求出月销量Q(百件)与销售价格P(元)的关系式,显然是一个分段函数;再将些函数代入该店月利润余额为L(元)(由题意可得得L=Q(P-14)×100-3600-2000),从而月利润余额是关于价格P的一个分段函数;每一段又都是一个关于P的二次函数,利用配方法求出各段的最大,取两个最大值中的最大者即为所求;此问题注意统一单位;(2)设最早可望在n年后脱贫,由(1)可知月利润扣除职工最低生活费的余额最大值,则可计算得每年的余额值乘以n后大于或等于债务:50000+58000即可,解此不等式可得问题答案.注意要将数学解答的结果还原成实际应用问题的答案.
试题解析:设该店月利润余额为L,则由题设得L=Q(P-14)×100-3600-2000, ①
由销量图易得

=
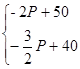
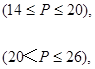
代入①式得L=
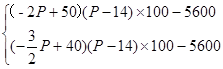
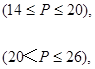
(1)当
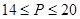
时,
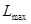
=450元,此时

元,当20<P≤26时,L
max=
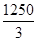
元,此时P=
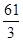
元。故当P=19.5元时,月利润余额最大,为450元,
(2)设可在n年内脱贫,
依题意有

解得 n≥20
即最早可望在20年后脱贫

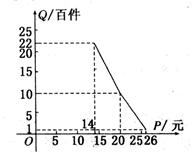
 =
=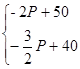
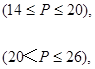
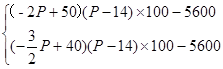
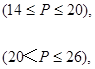
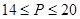 时,
时,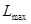 =450元,此时
=450元,此时 元,当20<P≤26时,Lmax=
元,当20<P≤26时,Lmax=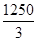 元,此时P=
元,此时P=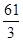 元。故当P=19.5元时,月利润余额最大,为450元,
元。故当P=19.5元时,月利润余额最大,为450元, 解得 n≥20
解得 n≥20
