
【题目】已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,﹣3),点P的横坐标为14,且 ![]() ,点Q是边AB上一点,且
,点Q是边AB上一点,且 ![]() .
.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:设P(14,y),则 ![]() ,由
,由 ![]() ,得(14,y)=λ(﹣8,﹣3﹣y),解得
,得(14,y)=λ(﹣8,﹣3﹣y),解得 ![]() ,所以点P(14,﹣7)
,所以点P(14,﹣7)
(2)解:设点Q(a,b),则 ![]() ,又
,又 ![]() ,则由
,则由 ![]() ,得3a=4b①又点Q在边AB上,所以
,得3a=4b①又点Q在边AB上,所以 ![]() ,即3a+b﹣15=0②
,即3a+b﹣15=0②
联立①②,解得a=4,b=3,所以点Q(4,3).
(3)解:因为R为线段OQ上的一个动点,故设R(4t,3t),且0≤t≤1,则, ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() =
= ![]() ,故
,故 ![]() 的取值范围为
的取值范围为 ![]()
【解析】(1)先设P(14,y),分别表示 ![]() ,
, ![]() 然后由
然后由 ![]() ,建立关于y的方程可求y.(2)先设点Q(a,b),则可表示向量
,建立关于y的方程可求y.(2)先设点Q(a,b),则可表示向量 ![]() ,由
,由 ![]() ,可得3a=4b,再由点Q在边AB上可得
,可得3a=4b,再由点Q在边AB上可得 ![]() ①②,从而可解a,b,进而可得Q的坐标.(3)由R为线段OQ上的一个动点可设R(4t,3t),且0≤t≤1,则有分别表示
①②,从而可解a,b,进而可得Q的坐标.(3)由R为线段OQ上的一个动点可设R(4t,3t),且0≤t≤1,则有分别表示 ![]() ,
, ![]() ,由向量的数量积整理可得
,由向量的数量积整理可得 ![]() ,利用二次函数的知识可求取值范围.
,利用二次函数的知识可求取值范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x |
|
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式.
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为 ![]() ,当
,当 ![]() 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.若 ![]() 与
与 ![]() 互为负向量,则
互为负向量,则 ![]() +
+ ![]() =0
=0
B.若 ![]()
![]() =0,则
=0,则 ![]() =
= ![]() 或
或 ![]() =
= ![]()
C.若 ![]() ,
, ![]() 都是单位向量,则
都是单位向量,则 ![]()
![]() =1
=1
D.若k为实数且k ![]() =
= ![]() ,则k=0或
,则k=0或 ![]() =
= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养正中学新校区内有一块以O为圆心,R(单位:米)为半径的半圆形荒地(如图),校总务处计划对其开发利用,其中弓形BCD区域(阴影部分)用于种植观赏植物,△OBD区域用于种植花卉出售,其余区域用于种植草皮出售。已知种植观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元。
(1)设![]() (单位:弧度),用
(单位:弧度),用![]() 表示弓形BCD的面积
表示弓形BCD的面积![]()
(2)如果该校总务处邀请你规划这块土地。如何设计![]() 的大小才能使总利润最大?并求出该最大值
的大小才能使总利润最大?并求出该最大值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( ) 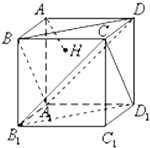
A.点H是△A1BD的垂心
B.AH的延长线经过点C1
C.AH垂直平面CB1D1
D.直线AH和BB1所成角为45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,g(x)=ax,(a∈R).
(1)若函数y=f(x)是偶函数,求出符合条件的实数a的值;
(2)若方程f(x)=g(x)有两解,求出实数a的取值范围;
(3)若a>0,记F(x)=g(x)f(x),试求函数y=F(x)在区间[1,2]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:
|
| 700 |
|
|
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年9月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数有相关关系,如表3:
指数有相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店9月份平均每天的收入.
(附参考公式: ![]() ,其中
,其中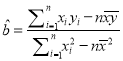 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() (其中a,b为常数)的图象经过(1,2),(2,
(其中a,b为常数)的图象经过(1,2),(2, ![]() )两点.
)两点.
(1)求函数f(x)的解析式;
(2)判断f(x)的奇偶性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com