【答案】
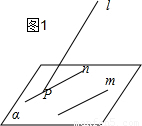
分析：A．不存在与l平行的直线，可用反证法证明：设l∩α=P，假设α内存在与l平行的直线m，则m不过点P，在α内过点P作n∥m，则n∥l，得出矛盾，故假设不成立，即可判断出；
B．如图2，在平面α内存在无数条与l垂直的直线．证明如下：设l∩α=A，在l取异于点A的P，过PB⊥α，垂足为B，在α内作m⊥AB，由三垂线定理可得m⊥l，则在α所有与m平行的直线n都与l垂直，即在平面α内存在无数条与l垂直的直线，据此即可判断出．
C．由B可知：在平面α内存在无数条与l垂直的直线．因此C不正确．
D．由A可知：不存在与l平行的直线，因此D不正确．
解答：解：A．不存在与l平行的直线，可用反证法证明：设l∩α=P，假设α内存在与l平行的直线m，则m不过点P，在α内过点P作n∥m，则n∥l，得出矛盾，故假设不成立，因此A不正确；
B．如图2，在平面α内存在无数条与l垂直的直线．证明如下：
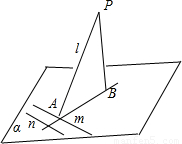
设l∩α=A，在l取异于点A的P，过PB⊥α，垂足为B，在α内作m⊥AB，由三垂线定理可得m⊥l，
则在α所有与m平行的直线n都与l垂直，即在平面α内存在无数条与l垂直的直线．因此B不正确．
C．由B可知：在平面α内存在无数条与l垂直的直线．因此C不正确．
D．由A可知：不存在与l平行的直线，因此D不正确．
综上可知：只有A正确．
故选A．
点评：熟练掌握线面平行于垂直的判定定理和性质定理、反证法、三垂线定理是解题的关键．
