练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知数列{an}满足an=3an-1+5，a1=1，求数列{an}的通项公式．

    分析 把已知数列递推式变形，可得数列{${a}_{n}+\frac{5}{2}$}构成以$\frac{7}{2}$为首项，以3为公比的等比数列，求出等比数列的通项公式后可得数列{an}的通项公式．

    解答 解：由an=3an-1+5，得
    ${a}_{n}+\frac{5}{2}=3（{a}_{n-1}+\frac{5}{2}）$，
    又${a}_{1}+\frac{5}{2}=\frac{7}{2}≠0$，
    ∴$\frac{{a}_{n}+\frac{5}{2}}{{a}_{n-1}+\frac{5}{2}}=3（n≥2）$，
    ∴数列{${a}_{n}+\frac{5}{2}$}构成以$\frac{7}{2}$为首项，以3为公比的等比数列，
    则${a}_{n}+\frac{5}{2}=\frac{7}{2}•{3}^{n-1}$，
    ∴${a}_{n}=\frac{7}{2}•{3}^{n-1}-\frac{5}{2}$．

    点评 本题考查数列递推式，考查了等比关系的确定，训练了等比数列通项公式的求法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知命题p：x2-ax+1=0有两个实根，q：函数y=x2+ax+b在[1，+∞）上为增函数，若命题“p∧q”为真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=log2（2|x+1|+|2x+m|-m）
    （I）当m=6时，求函数f（x）的定义域；
    （Ⅱ）当函数f（x）的值域为R时，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知向量$\overrightarrow{a}$=（sinθ，cosθ），$\overrightarrow{b}$=（3，-4），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则tan2θ=±$\frac{24}{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=$\frac{ax+b}{1+{x}^{2}}$是定义在（-1，1）上的奇函数，且f（$\frac{1}{2}$）=$\frac{2}{5}$．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）证明f（x）在（-1，1）上是增函数；
    （Ⅲ）若f（x）-3t+1＞0在（-1，0）上恒成立，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

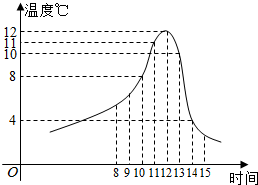    3．某食品的保鲜时间t（单位：小时）与储藏温度x（单位：℃）满足函数关系t=$\left\{\begin{array}{l}{64，x≤0}\\{{2}^{kx+6}，x＞0}\end{array}\right.$且该食品在4℃的保鲜时间是16小时．已知甲在某日上午10时购买了该食品，并将其遗放在室外，且此日的室外温度随时间变化如图所示，给出以下四个结论：
    ①该食品在6℃的保鲜时间是8小时；
    ②当x∈[-6，6]时，该食品的保鲜时间t随看x增大而逐渐减少；
    ③到了此日13时，甲所购买的食品还在保鲜时间内；
    ④到了此日14时，甲所购买的食品已然过了保鲜时间
    其中，所有正确结论的序号是①④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=lnx+ax2，g（x）=$\frac{1}{x}$+x+b，且直线y=-$\frac{1}{2}$是函数f（x）的一条切线，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．用列举法表示A={x|-4＜x＜2，x∈Z}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知函数f（x）=$\left\{\begin{array}{l}{e^x+a，x≤0}\\{3x-1，x＞0}\end{array}\right.$（a∈R），若函数f（x）在R上有两个零点，则a的取值范围是（　　）
    A．（-∞，-1）B．（-∞，0）C．（-1，0）D．[-1，0）

    查看答案和解析>>

    同步练习册答案