Question

【题目】某校开展“读好书，好读书”活动，要求本学期每人至少读一本课外书，该校高一共有100名学生，他们本学期读课外书的本数统计如图所示． （Ⅰ）求高一学生读课外书的人均本数；
（Ⅱ）从高一学生中任意选两名学生，求他们读课外书的本数恰好相等的概率；
（Ⅲ）从高一学生中任选两名学生，用ζ表示这两人读课外书的本数之差的绝对值，求随机变量ζ的分布列及数学期望E．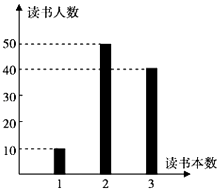

Answer 1

【答案】解：（Ⅰ）由图知读课外书1本、2本、3本的学生人数分别为10，50和40， ∴高一学生读课外书的人均本数为：
=2.3．
（Ⅱ）从高一学生中任选两名学生，他们读课外书的本数恰好相等的概率为：
p= = ．
（Ⅲ）从高一学生中任选两名学生，
记“这两人中一人读1本书，另一人读2本书”为事件A，
“这两人中一人读2本书，另一人读3本书”为事件B，
“这两人中一人读1本书，另一人读3本书”为事件C，
从高一学生中任选两名学生，用ζ表示这两人读课外书的本数之差的绝对值，
则ζ的可能取值为0，1，2，
P（ζ=1）= = ，
P（ζ=1）=P（A）+P（B）= + = ，
P（ζ=2）=P（C）= = ，
∴ζ的分布列为：

ζ	1	1	2
P

E（ζ）= =
【解析】（Ⅰ）由图知读课外书1本、2本、3本的学生人数分别为10，50和40，由此能求出高一学生读课外书的人均本数．（Ⅱ）从高一学生中任选两名学生，利用互斥事件概率加法公式能求出他们读课外书的本数恰好相等的概率．（Ⅲ）从高一学生中任选两名学生，用ζ表示这两人读课外书的本数之差的绝对值，则ζ的可能取值为0，1，2，分别求出相应的概率，由此能求出随机变量ζ的分布列及数学期望Eζ．
【考点精析】掌握离散型随机变量及其分布列是解答本题的根本，需要知道在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．