练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如下图，正方形SG1G2G3中，E、F分别是G1G2、G2G3的中点，D是EF的中点，现在沿SE、SF及EF把这个正方形折成一个四面体，使G1、G2、G3三点重合，重合后的点记为G，则在四面体S－EFG中必有

    [　　]

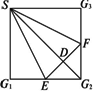
    A．SG⊥△EFG所在平面

    B．SD⊥△EFG所在平面

    C．GF⊥△SEF所在平面

    D．GD⊥△SEF所在平面

    答案：A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

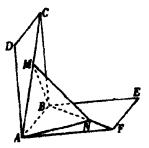
    如下图，正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM＝BN＝a（0＜a＜）．

    　　（Ⅰ）求MN的长；

    　　（Ⅱ）当a为何值时，MN的长最小；

    　　（Ⅲ）当MN长最小时，求面MNA与面MNB所成的二面角a 的大小．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    如下图，正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM＝BN＝a（0＜a＜）．

    　　（Ⅰ）求MN的长；

    　　（Ⅱ）当a为何值时，MN的长最小；

    　　（Ⅲ）当MN长最小时，求面MNA与面MNB所成的二面角a 的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (2006黄冈)如下图，正方形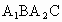的边长为4，D是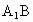的中点，E是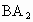上的点，将△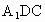及△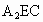分别沿DC和EC折起，使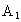、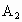重合于A，且二面角A－DC－E为直二面角．

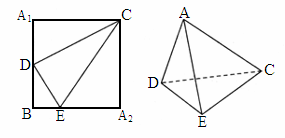
    (1)求证：CD⊥DE；

    (2)求AE与面DEC所成角的正弦值；

    (3)求点D到平面AEC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图,在正方形ABCD中,E,F分别是边BC,CD的中点,H是EF的中点,现沿AE,AF,EF把这个正方形折成一个几何体,使B,C,D三点重合于G,则下列结论中正确的是(    )

    A.AG⊥平面EFG              B.AH⊥平面EFG

    C.GF⊥平面AEF              D.GH⊥平面AEF

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在如下图的正方形中随机撒一把豆子,用计算机随机模拟的方法估算圆周率的值.

    查看答案和解析>>

    同步练习册答案