
| 日期 | PM2.5浓度 | 日期 | PM2.5浓度 | 日期 | PM2.5浓度 |
| 11-1 | 137 | 11-11 | 144 | 11-21 | 40 |
| 11-2 | 143 | 11-12 | 166 | 11-22 | 42 |
| 11-3 | 145 | 11-13 | 197 | 11-23 | 35 |
| 11-4 | 193 | 11-14 | 194 | 11-24 | 53 |
| 11-5 | 133 | 11-15 | 219 | 11-25 | 88 |
| 11-6 | 22 | 11-16 | 41 | 11-26 | 29 |
| 11-7 | 22 | 11-17 | 90 | 11-27 | 199 |
| 11-8 | 57 | 11-18 | 46 | 11-28 | 287 |
| 11-9 | 111 | 11-19 | 80 | 11-29 | 291 |
| 11-10 | 134 | 11-20 | 67 | 11-30 | 452 |
| 空气质量指数类别 | PM2.5 24小时浓度均值 | 频数 | 频率 |
| 优 | 0-35 | 4 | $\frac{2}{15}$ |
| 良 | 36-75 | 7 | $\frac{7}{30}$ |
| 轻度污染 | 76-115 | 4 | |
| 中度污染 | 116-150 | 6 | |
| 重度污染 | 151-250 | ||
| 严重污染 | 251-500 | ||
| 合计 | / | 30 | 1 |
分析 (Ⅰ)由已知条件能作出频率分布表.
(Ⅱ)由已知条件列举法能求出拔河比赛能正常进行的概率.
解答 解(Ⅰ)由已知作出频率分布表为:
| 空气质量指数类别 | PM2.5 24小时浓度均值 | 频数 | 频率 |
| 优 | 0-35 | 4 | $\frac{2}{15}$ |
| 良 | 36-75 | 7 | $\frac{7}{30}$ |
| 轻度污染 | 76-115 | 4 | $\frac{2}{15}$ |
| 中度污染 | 116-150 | 6 | $\frac{1}{5}$ |
| 重度污染 | 151-250 | 6 | $\frac{1}{5}$ |
| 严重污染 | 251-500 | 3 | $\frac{1}{10}$ |
| 合计 | 30 | 1 |
点评 本题考查频率分布列的作法,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:填空题
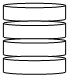 小明有4枚完全相同的硬币,每个硬币都分正反两面.他把4枚硬币叠成一摞(如图),则所有相邻两枚硬币中至少有一组同一面不相对的概率是$\frac{7}{8}$.
小明有4枚完全相同的硬币,每个硬币都分正反两面.他把4枚硬币叠成一摞(如图),则所有相邻两枚硬币中至少有一组同一面不相对的概率是$\frac{7}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命題“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | “a>1且b>1”是“ab>1”的充分不必要条件 | |
| C. | 若命题p:?x0∈N,2${\;}^{{x}_{0}}$>1000,则¬p:?x∈N,2x≤1000 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com