Question

4．已知函数f（x）=x|x-2a|
（1）化简f（x）；
（2）试确定a的取值范围，使函数f（x）在区间[2，+∞）上是单调增函数；
（3）在（2）的条件下，求函数f（x）在区间[1，2]上的最大值g（a）．

Answer 1

分析 （1）讨论x从而可去掉绝对值号，便可化简f（x）；
（2）可以看出f（x）=x²-2ax和f（x）=-x²+2ax的对称轴都为x=a，可以画出a＞0，a=0，和a＜0时的函数f（x）的图象，根据图象便可得出要使得f（x）在区间[2，+∞）上单调递增，需2a≤2，这样便可得出a的取值范围；
（3）可结合图象，讨论a：分2a=2，1＜2a＜2，和2a≤1三种情况，然后可结合图象，比较端点f（1），f（2）的大小，以及根据f（x）在[1，2]上的单调性便可求出每种情况下函数f（x）在区间[1，2]上的最大值g（a）．

解答 解：（1）$f（x）=\left\{\begin{array}{l}{{x}^{2}-2ax}&{x≥2a}\\{-{x}^{2}+2ax}&{x＜2a}\end{array}\right.$；
（2）x≥2a时，f（x）=x²-2ax，f（x）的对称轴为x=a；
x＜2a时，f（x）=-x²+2ax，f（x）的对称轴为x=a，a＞0时f（x）的图象如下所示：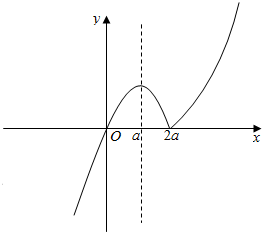

∴要使f（x）在[2，+∞）上为单调增函数，则：0＜2a≤2；
∴0＜a≤1；
可看出当a≤0时，显然满足f（x）在[2，+∞）上单调递增；
∴a的取值范围为（-∞，1]；
（3）1）若2a=2，即a=1时，g（a）=f（1）=2a-1；
2）若1＜2a＜2，即$\frac{1}{2}＜a＜1$时，f（1）=2a-1，f（2）=4-4a；
∴f（1）-f（2）=6a-5；
∴$①\frac{5}{6}≤a＜1$时，g（a）=f（1）=2a-1；
②$\frac{1}{2}＜a＜\frac{5}{6}$时，g（a）=f（2）=4-4a；
3）若2a≤1，即a$≤\frac{1}{2}$时，f（x）在[1，2]上单调递增；
∴g（a）=f（2）=4-4a；
∴综上得，$g（a）=\left\{\begin{array}{l}{2a-1}&{\frac{5}{6}≤a≤1}\\{4-4a}&{a＜\frac{5}{6}}\end{array}\right.$．

点评 考查含绝对值函数的处理方法：去绝对值号，二次函数的对称轴，二次函数的单调性，根据函数图象判断函数单调性的方法，结合分段函数图象求分段函数最大值的方法，根据函数的单调性求分段函数在闭区间上最大值的方法．