
【题目】已知点![]() ,椭圆
,椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的方程.
的方程.
【答案】(1) ![]() 的方程为
的方程为![]() ;(2)
;(2) ![]() 的方程为
的方程为![]() 或
或![]() .
.
【解析】试题分析:(1)首先设![]() ,根据直线
,根据直线![]() 的斜率可列式
的斜率可列式![]() ,求
,求![]() 。再根据离心率求
。再根据离心率求![]() ,最后根据
,最后根据![]() 求
求![]() ,得到椭圆方程;(2)设直线的方程是
,得到椭圆方程;(2)设直线的方程是![]() 与椭圆方程联立后得到根与系数的关系,求弦长
与椭圆方程联立后得到根与系数的关系,求弦长![]() ,以及点
,以及点![]() 到直线
到直线![]() 的距离,将面积表示为
的距离,将面积表示为![]() 的函数,换元后求函数的最值,以及取得最值时的直线方程.
的函数,换元后求函数的最值,以及取得最值时的直线方程.
试题解析:(1)设![]() ,由条件知,
,由条件知,![]() ,得
,得![]()
又![]() ,所以
,所以![]() ,
,![]()
故![]() 的方程为
的方程为![]()
(2)当![]() 轴时不合题意,
轴时不合题意,
故可设![]() :
:![]() ,
,![]() ,
,![]()
将![]() 代入
代入![]() 得
得![]() ,
,
当![]() ,即
,即![]() 时,
时,
![]()
从而![]()
![]()
又点![]() 到直线
到直线![]() 的距离
的距离![]()
所以![]() 的面积
的面积
![]()
设![]() ,则
,则![]() ,
,![]()
因为![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立,满足
时等号成立,满足![]()
所以,当![]() 的最大面积时,
的最大面积时,![]() ,
,![]() 的方程为
的方程为![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,左顶点为
,左顶点为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条相互垂直的直线分别与椭圆
作两条相互垂直的直线分别与椭圆![]() 交于(不同于点
交于(不同于点![]() 的)
的)![]() 两点.试判断直线
两点.试判断直线![]() 与
与![]() 轴的交点是否为定点,若是,求出定点坐标;若不是,请说明理由.
轴的交点是否为定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD一边CD所在直线的方程为x+3y-13=0,对角线AC,BD的交点为P(1,5),求正方形ABCD其他三边所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017湖北部分重点中学高三联考)从编号为001,002,…,500的500个产品中用系统抽样的方法抽取一个样本,已知样本编号从小到大依次为007,032,…,则样本中最大的编号应该为( )
A. 483 B. 482
C. 481 D. 480
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)求函数![]() 的单调区间;
的单调区间;
(2)试问:函数![]() 图像上是否存在不同两点
图像上是否存在不同两点![]() ,使得
,使得![]() 在
在![]() 处的切线
处的切线![]() 平行于直线
平行于直线![]() ,若存在,求出
,若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x+1|<1},B={x|( ![]() )x﹣2≥0},则A∩RB=( )
)x﹣2≥0},则A∩RB=( )
A.(﹣2,﹣1)
B.(﹣2,﹣1]
C.(﹣1,0)
D.[﹣1,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为[50,60),[60,70),[70,80),[80,90),[90,100],据此解答如下问题. 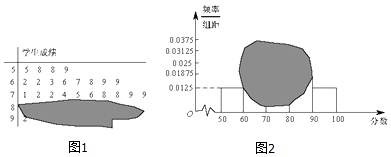
(Ⅰ)求全班人数及分数在[80,100]之间的频率;
(Ⅱ)现从分数在[80,100]之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在[90,100]的份数为X,求X的分布列和数学望期.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com