练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知扇形的周长为8cm，则该扇形面积的最大值为________cm2.

     

    4

    【解析】设扇形半径为rcm，弧长为lcm，则2r＋l＝8，S＝rl＝r×(8－2r)＝－r2＋4r＝－(r－2)2＋4，所以Smax＝4(cm2)

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第三章第5课时练习卷（解析版） 题型：填空题

    函数f(x)＝sinxcosx的最小正周期是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第三章第3课时练习卷（解析版） 题型：填空题

    函数y＝2sinx的值域是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第三章第2课时练习卷（解析版） 题型：解答题

    已知关于x的方程2x2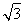－(＋1)x＋m＝0的两根为sinθ和cosθ，且θ∈(0，2π)．

    (1)求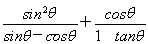的值；

    (2)求m的值；

    (3)求方程的两根及此时θ的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第三章第1课时练习卷（解析版） 题型：解答题

    已知在半径为10的圆O中，弦AB的长为10.

    (1)求弦AB所对的圆心角α的大小；

    (2)求α所在的扇形的弧长l及弧所在的弓形的面积S.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第三章第1课时练习卷（解析版） 题型：填空题

    已知点P(tanα，cosα)在第二象限，则角α的终边在第________象限．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第七章第3课时练习卷（解析版） 题型：解答题

    设数列{an}：1，－2，－2，3，3，3，－4，－4，－4，－4，…，(－1)k－1k，…，(－1)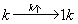，即当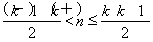(k∈N*)时，an＝(－1)k－1k，记Sn＝a1＋a2＋…＋an(n∈N*)，用数学归纳法证明Si(2i＋1)＝－i(2i＋1)(i∈N*)．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第七章第2课时练习卷（解析版） 题型：填空题

    已知a>b>c，且a＋b＋c＝0，求证：a.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第一章第2课时练习卷（解析版） 题型：填空题

    设集合A＝{5，log2(a＋3)}，集合B＝{a，b}．若A∩B＝{2}，则A∪B＝________．

     

    查看答案和解析>>

    同步练习册答案