
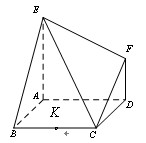
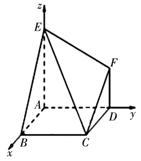
如图,已知多面体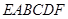 的底面
的底面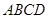 是边长为
是边长为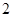 的正方形,
的正方形,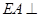 底面
底面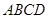 ,
,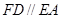 ,且
,且 .
.
(Ⅰ)求多面体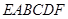 的体积;
的体积;
(Ⅱ)求直线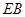 与平面
与平面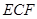 所成角的正弦值;
所成角的正弦值;
(Ⅲ)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面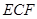 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅰ)(Ⅰ)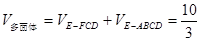 .
.
(Ⅱ)设直线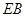 与平面
与平面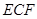 所成角为
所成角为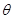 ,
, 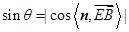


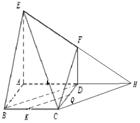
(Ⅲ)利用三角形中位线定理,取线段DC的中点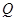 ,连接即为所求.
,连接即为所求.
【解析】
试题分析:(Ⅰ)(Ⅰ)连接ED,利用“分割法”计算得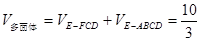 .
.
(Ⅱ)以点A为原点,AB所在的直线为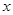 轴,AD所在的直线为
轴,AD所在的直线为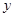 轴,建立空间直角坐标系.确定得到A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),及
轴,建立空间直角坐标系.确定得到A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),及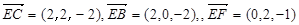 .
.
利用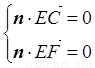 确定平面
确定平面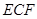 的一个法向量为
的一个法向量为 .
.
设直线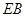 与平面
与平面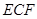 所成角为
所成角为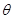 ,
,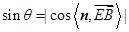


(Ⅲ)取线段DC的中点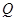 ;连接
;连接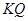 ,则直线
,则直线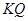 即为所求.
即为所求.
试题解析:(Ⅰ)如图,连接ED,
∵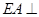 底面
底面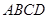 且
且 ,∴
,∴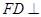 底面
底面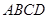 ,
,
∴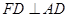 ,
,
∵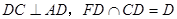 ,
,
∴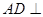 面
面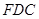 ,
1分
,
1分
∴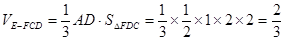 ,
2分
,
2分
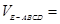
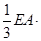
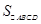
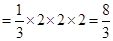 ,
3分
,
3分
∴多面体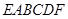 的体积
的体积
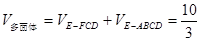 . 5分
. 5分
(Ⅱ)以点A为原点,AB所在的直线为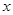 轴,AD所在的直线为
轴,AD所在的直线为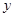 轴,建立空间直角坐标系,如图.由已知可得A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),
轴,建立空间直角坐标系,如图.由已知可得A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),
所以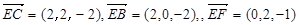 7分
7分
设平面ECF的法向量为 ,
,
则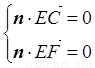 得:
得: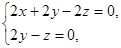
取y=1,得平面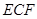 的一个法向量为
的一个法向量为 9分
9分
设直线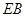 与平面
与平面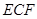 所成角为
所成角为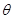 ,
,
所以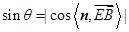

 11分
11分
(Ⅲ)取线段CD的中点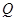 ;连接
;连接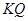 ,直线
,直线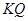 即为所求.
12分
即为所求.
12分
图上有正确的作图痕迹 13分

考点:1、平行关系,2、垂直关系,3、空间向量的应用,4、角及体积的计算.


科目:高中数学 来源: 题型:
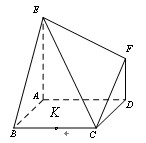
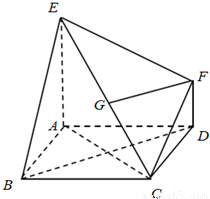
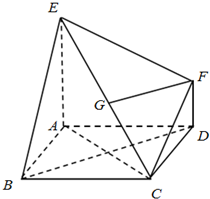 如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.
如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建福州市毕业班质量检查文科数学试卷(解析版) 题型:解答题
如图,已知多面体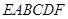 的底面
的底面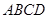 是边长为
是边长为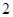 的正方形,
的正方形,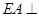 底面
底面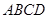 ,
,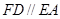 ,且
,且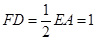 .
.
(Ⅰ )求多面体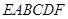 的体积;
的体积;
(Ⅱ )求证:平面EAB⊥平面EBC;
(Ⅲ)记线段CB的中点为K,在平面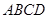 内过K点作一条直线与平面
内过K点作一条直线与平面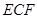 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省厦门市高一(下)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com