练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

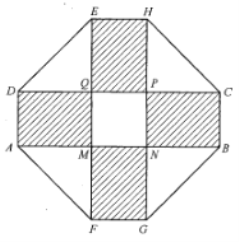
    【题目】某小区要建一个八边形的休闲区，如图所示，它的主要造型平面图是由两个相同的矩形和构成的面积为的十字形区域.计划在正方形上建一个花坛，造价为4200元/，在四个相同的矩形（图中阴影部分）上铺设花岗岩地面，造价为210元/，再在四个等腰直角三角形上铺设草坪，造价为80元/.求当的长度为多少时，建设这个休闲区的总价最低.

    【答案】当的长度为时，建设休闲区总价最低

    【解析】

    由题意，十字形区域面积固定，造型随着的改变而改变，从而使得总费用也随之变化. 设的长度为米，建设休闲区的总价为y元.计算出中间正方形区域面积、四个矩形面积之和、四块等腰直角三角形的面积之和，即可求出总价y关于的函数解析式，再利用基本不等式求最小值，即可求出的值.

    设的长度为，建设休闲区的总价为y元，

    则中间正方形区域面积为，四个矩形面积之和为，，四块等腰直角三角形的面积之和为.

    ∴

    .

    由，，可得.

    ，

    当且仅当，即时，等号成立.

    所以，当的长度为时，建设休闲区总价最低.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn，a1＝1，an＋1＝2Sn＋1(n∈N*)，等差数列{bn}中，bn＞0(n∈N*)，且b1＋b2＋b3＝15，又a1＋b1、a2＋b2、a3＋b3成等比数列．

    (1)求数列{an}、{bn}的通项公式；

    (2)求数列{an·bn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）已知点A，B的坐标分别为（3，0），（-3，0），直线AP，BP相交于点P，且它们的斜率之积是-2，求动点P的轨迹方程．

    （2）设P（x，y），直线l1：x+y=0，l2：x-y=0．若点P到l1的距离与点P到l2的距离之积为2，求动点P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，圆锥PO中，AB是圆O的直径，且AB＝4，C是底面圆O上一点，且AC＝2，点D为半径OB的中点，连接PD.

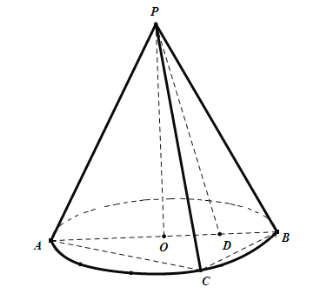
    （1）求证：PC在平面APB内的射影是PD；

    （2）若PA＝4，求底面圆心O到平面PBC的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，圆C的参数方程为(θ为参数)，直线l经过点P(1,2)，倾斜角α＝ ．

    (1)写出圆C的普通方程和直线l的参数方程；

    (2)设直线l与圆C相交于A，B两点，求|PA|·|PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知从1开始的连续奇数蛇形排列形成宝塔形数表，第一行为1，第二行为3，5，第三行为7，9，11，第四行为13，15，17，19，…，如图所示，在宝塔形数表中位于第行、第列的数记为，比如，，．若，则______．

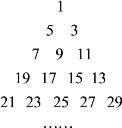
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】研究函数的定义域、奇偶性、单调性和最值，并作出它的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

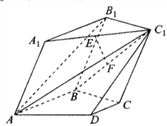
    【题目】在如图所示的多面体中，平面平面，四边形为边长为2的菱形， 为直角梯形，四边形为平行四边形，且， ， .

    （1）若， 分别为， 的中点，求证： 平面；

    （2）若， 与平面所成角的正弦值为，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知长方形中， 的中点，将沿折起，使得平面平面.

    （1）求证： ；

    （2）设，当为何值时，二面角的余弦值.

    查看答案和解析>>

    同步练习册答案