



 ,sin25°+sin265°+sin2125°=
,sin25°+sin265°+sin2125°= .我们可以发现等式左边参加累加的三个均为正弦的平方,且三个角组成一个以60°为公差的等差数列,右边是常数,由此不难得到结论.
.我们可以发现等式左边参加累加的三个均为正弦的平方,且三个角组成一个以60°为公差的等差数列,右边是常数,由此不难得到结论. ,
, .
. .
. +
+ +
+
 -
- [cos(2α-120°)+cos2α+cos(2α+120°)]
[cos(2α-120°)+cos2α+cos(2α+120°)] =右边.
=右边.

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
已知向量=(cos25°,sin25°),=(sin20°,cos20°),若t是实数,且=+t,则||的最小值为 ( )
A. B.1 C. D.
查看答案和解析>>
科目:高中数学 来源:2011年4月北京市人大附中模块考试数学试卷(必修4)(解析版) 题型:选择题
 =(cos85°,sin85°),
=(cos85°,sin85°), =(cos25°,sin25°),则|
=(cos25°,sin25°),则| +
+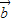 |的值为( )
|的值为( )
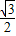

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com