
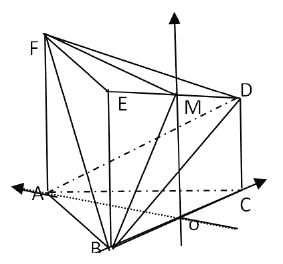
【题目】在如图所示的几何体中,正方形![]() 所在的平面与正三角形
所在的平面与正三角形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求面![]() 与面
与面![]() 所成锐二面角的大小.
所成锐二面角的大小.

【答案】(1)见解析(2) 60°
【解析】试题分析:
(1)连接AE交BF于点N,连接MN,MN∥AD,由此能证明AD∥平面BFM.(2)推导出BE⊥AB,从而BE⊥平面ABC,取BC的中点O,连接OM,以O为坐标原点建立空间直角坐标系,利用向量法能求出二面角E-BM-F的余弦值.
解析:
(1)证明:

连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
因为![]() 是正方形,所以
是正方形,所以![]() 是
是![]() 的中点,
的中点,
又![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)解法一:
因为![]() 是正方形,所以
是正方形,所以![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() ,所以取
,所以取![]() 的中点
的中点![]() .连接
.连接![]() ,则
,则![]() 平面
平面![]() ,因为
,因为![]() 是正三角形,所以
是正三角形,所以![]() ,
,
所以以![]() 为坐标原点,
为坐标原点, ![]() 所在直线为
所在直线为![]() 轴建立如图所示的空间直角坐标系:设
轴建立如图所示的空间直角坐标系:设![]() ,
,
则![]() ,
,
![]() ,
,
设面![]() 的法向量为
的法向量为![]() ,
,
则 ,
,
令![]() ,则
,则![]() ,
,
∴ ,
,
设面![]() 的法向量为
的法向量为![]() ,则
,则
 ,
,
令![]() ,则
,则![]() , ∴
, ∴ ,
,
 ,因为求面
,因为求面![]() 与面
与面![]() 所成锐二面角, ∴平面
所成锐二面角, ∴平面![]() 与平面
与平面![]() 所成二面角的平面角为60°.
所成二面角的平面角为60°.
(2)解法二:

因为直线![]() ,所以面
,所以面![]() 与面
与面![]() 的交线
的交线![]() 与之平行,即
与之平行,即![]() ,
,
分别取![]() 的中点
的中点![]() ,连
,连![]() ,
,
因为![]() ,且
,且![]() ,根据射影定理,所以
,根据射影定理,所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以为所求锐二面角的平面角,
设![]() ,则
,则![]() ,
,
所以![]() ,
,
所以![]() 为正三角形,所以
为正三角形,所以![]() ,
,
所以为所示锐二面角为60°.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某化工厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料,生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示:
配料 原料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车品乙种肥料,产生的利润为3万元、分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料,求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求证:“如果直线![]() 过点
过点![]() ,那么
,那么![]() ”是真命题;
”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() .
.
(1)证明:BC![]() A1D;
A1D;
(2)求二面角A-CC1-B的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD—A1B1C1D1中,E是BC的中点,
平面B1ED交A1D1于F。
(1)指出F在A1D1上的位置,并说明理由;
(2)求直线A1C与DE所成的角的余弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图
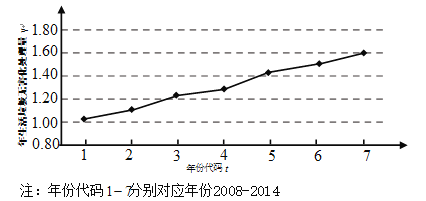
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请建立
的关系,请建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(2)预测2018年我国生活垃圾无害化处理量.
附注:
参考公式:设具有线性相关关系的两个变量![]() 的一组观察值为
的一组观察值为![]() ,
,
则回归直线方程![]() 的系数为:
的系数为:
 ,
, ![]() .
.
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若过点![]() ),可作曲线
),可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围;
的取值范围;
(3)若对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,都有
,都有![]() ,求实数
,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com