【题目】某公司有男性职工64名，一次体检后，将他们的体重（单位：kg）分组为：
，
，
，
，
，绘制出频率分布直方图如图，图中从左到右的前3个小组的频率之比为
.
（1）求这64名男职工中，体重小于60kg的人数；
（2）从体重在
kg范围的男职工中用分层抽样的方法选取6名，再从这6名男职工中随机选取2名，记“至少有一名男职工体重大于65kg”为事件
，求事件发生的概率.
【答案】（1）24；（2）
.
【解析】
（1）设50~55kg这个小组对应的频率为a，依题意得到方程组，解得即可；
（2）首先求出体重在60~65kg与65~70kg的人数，分别记他们为
，
，
，
，
，
，利用列举法列出所有可能结果，最后再利用古典概型的概率公式计算可得；
解：（1）设50~55kg这个小组对应的频率为a.
65~75kg对应的频率为
，
，解得
.
50~60kg对应的频率为0.375，从而所求人数为
.
（2）男职工体重在60~65kg与65~70kg的频率之比为
，
这6名男职工体重在60~65kg与65~70kg的个数分别为4，2.
分别记他们为，，，，，，从中随机选取2名的所有情况为
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共15个基本事件，
其中事件A包含9个基本事件，
.
53随堂测系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知抛物线
：
，过抛物线焦点
且与
轴垂直的直线与抛物线相交于
、
两点，且
的周长为
.
（1）求抛物线的方程；
（2）若直线
过焦点且与抛物线相交于
、
两点，过点、分别作抛物线的切线
、
，切线与相交于点
，求：
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，若在定义域内存在
，使得
成立，则称为函数的局部对称点.
（1）若
且
，证明：函数
必有局部对称点；
（2）若函数
在定义域
内有局部对称点，求实数
的取值范围；
（3）若函数
在
上有局部对称点，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某电子科技公司由于产品采用最新技术，销售额不断增长，最近
个季度的销售额数据统计如下表（其中
表示
年第一季度，以此类推）：
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y（百万元） |
|
|
|
|
|
（1）公司市场部从中任选
个季度的数据进行对比分析，求这个季度的销售额都超过
千万元的概率；
（2）求
关于
的线性回归方程，并预测该公司
的销售额.
附：线性回归方程：
其中
，
参考数据：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题，拟定出台“延迟退休年龄政策”.为了了解人们对“延迟退休年龄政策”的态度，责成人社部进行调研.人社部从网上年龄在15～65岁的人群中随机调查100人，调查数据的频率分布直方图如图所示, 支持“延迟退休年龄政策”的人数与年龄的统计结果如表：
年龄（岁） |
|
|
|
|
|
支持“延迟退休年龄政策”人数 | 15 | 5 | 15 | 28 | 17 |
（I）由以上统计数据填写下面的
列联表；
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 总计 | |
支持 | |||
不支持 | |||
总计 |
（II）通过计算判断是否有
的把握认为以45岁为分界点的不同人群对“延迟退休年龄政策”的态度有差异.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式：
查看答案和解析>>
科目：高中数学 来源： 题型：
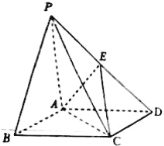
【题目】如图，在四棱锥P—ABCD中，底面ABCD是菱形，∠ABC＝60°，PA＝AC，PB＝PD＝
AC，E是PD的中点，求证：
（1）PB∥平面ACE；
（2）平面PAC⊥平面ABCD．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
