
 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖. ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 的分布列及
的分布列及 .
. ;(Ⅱ)分布列如下解析;
;(Ⅱ)分布列如下解析; .
. ,不都是是都是的对立面.所以假设有n个标有“美丽泉城行”则都是“美丽泉城行”的概率为
,不都是是都是的对立面.所以假设有n个标有“美丽泉城行”则都是“美丽泉城行”的概率为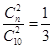 .计算出n的值.10-n就是印有“多彩十艺节”球的个数.即可求出抽奖者获奖的概率.(Ⅱ)本小题是一个超几何概型独立性实验.分布列和数学期望及方差公式.
.计算出n的值.10-n就是印有“多彩十艺节”球的个数.即可求出抽奖者获奖的概率.(Ⅱ)本小题是一个超几何概型独立性实验.分布列和数学期望及方差公式. .本题主要是考查概率知识,由生活背景引出数学知识.数学知识学以致用.
.本题主要是考查概率知识,由生活背景引出数学知识.数学知识学以致用. 个,不都是“美丽泉城行”标志为事件
个,不都是“美丽泉城行”标志为事件 ,
, ,由对立事件的概率:
,由对立事件的概率: ,
,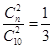
 ,故“多彩十艺节”标志卡共有4张
,故“多彩十艺节”标志卡共有4张 6分
6分 ~
~ ,
, 的分布列为
的分布列为 或
或 | 0 | 1 | 2 | 3 | 4 |
 |  |  |  |  |  |
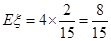
 12分
12分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 的分布列及数学期望
的分布列及数学期望查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加 组测试,丙、丁两人各自独立参加
组测试,丙、丁两人各自独立参加 组测试.已知甲、乙两人各自通过测试的概率均为
组测试.已知甲、乙两人各自通过测试的概率均为 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加 组测试,
组测试, 组共有6道试题,戊会其中4题.戊只能且必须选择4题作答,答对3题则竞聘成功.
组共有6道试题,戊会其中4题.戊只能且必须选择4题作答,答对3题则竞聘成功. 组测试通过的人数多于参加
组测试通过的人数多于参加 组测试通过的人数的概率;
组测试通过的人数的概率; 、
、 组测试通过的总人数为
组测试通过的总人数为 ,求
,求 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为: | 0 | 1 | 2 | 3 |
 | 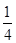 |  |  |  |
 ,
, 的值;
的值; 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.05 |
| [25,30) | ① | 0.20 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.30 |
| [40,45] | 10 | 0.10 |
| 合计 | 100 | 1.00 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com