
【题目】已知函数![]() .
.
(1)当![]() 时, 求曲线
时, 求曲线![]() 的极值;
的极值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若对任意![]() 及
及![]() 时, 恒有
时, 恒有![]() 成立, 求实数
成立, 求实数![]() 的取值范围.
的取值范围.
【答案】(1)极小值为![]() .(2)详见解析(3)
.(2)详见解析(3)![]()
【解析】
试题分析:(1)先求函数导数![]() ,再求导函数在定义区间上零点
,再求导函数在定义区间上零点![]() 。列表分析导函数符号变化规律得函数极值(2)由导函数为零点得
。列表分析导函数符号变化规律得函数极值(2)由导函数为零点得![]() ,根据零点是否在定义区间上,以及两个零点大小关系,分类讨论导函数符号变化规律,确定对应单调区间:共分四种情况
,根据零点是否在定义区间上,以及两个零点大小关系,分类讨论导函数符号变化规律,确定对应单调区间:共分四种情况![]() ,
,![]() ,
,![]() ,
,![]() (3)多变量不等式恒成立问题,一般方法仍为变量分离法,先分离x得
(3)多变量不等式恒成立问题,一般方法仍为变量分离法,先分离x得![]() ,即
,即![]() ;再分离m得
;再分离m得![]() 的最小值
的最小值
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时,![]() , 解得
, 解得![]() (舍去),
(舍去),![]() , 在
, 在![]() 上递减, 在
上递减, 在![]() 上递增, 所以
上递增, 所以![]() 的极小值为
的极小值为![]() .
.
(2)![]() ,令
,令![]() 可得
可得![]() .
.
①当![]() 时, 由
时, 由![]() 可得
可得![]() 在
在![]() 上单调递减, 由
上单调递减, 由![]() 可得
可得![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时, 由
时, 由![]() 可得
可得![]() 在
在![]() 上单调递减, 由
上单调递减, 由![]() 可得
可得![]() 得在
得在![]() 和
和![]() 上单调递增.
上单调递增.
③当![]() 时, 由
时, 由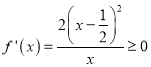 可得
可得![]() 在
在![]() 上单调递增.
上单调递增.
④当![]() 时, 由
时, 由![]() 可得
可得![]() 在
在![]() 上单调递减, 由
上单调递减, 由![]() 可得
可得![]() 得在
得在![]() 和
和![]() 上单调递增.
上单调递增.
(3)由题意可知, 对![]() 时, 恒有
时, 恒有![]() 成立, 等价于
成立, 等价于![]() ,
,
由(2)知, 当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() , 所以原题等价于
, 所以原题等价于![]() 时, 恒有
时, 恒有![]() 成立, 即
成立, 即![]() .在
.在![]() 时, 由
时, 由![]() ,故当
,故当![]() 时,
时,
![]() 恒成立,
恒成立,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设椭圆方程![]() +
+![]() =1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
=1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
(1)求椭圆方程;
(2)若M,N是椭圆C上的点,且直线OM与ON的斜率之积为﹣![]() ,是否存在动点P(x0,y0),若
,是否存在动点P(x0,y0),若![]() =
=![]() +2
+2![]() ,有x02+2y02为定值
,有x02+2y02为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行研究,用分层抽样方法从三所高校![]() 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)若从高校![]() 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题P;实数x满足x2-4ax+3a2<0,其中a>0;命题q:实数x满足x2-5x+6≤0
(1)若a=1,且![]() 为真命题,求实数x的取值范围。
为真命题,求实数x的取值范围。
(2)若p是q成立的必要不充分条件,求实数a 的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1+2x.
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图像;
(3)写出函数f(x)的单调区间及值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
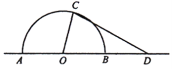
【题目】
如图,某城市有一块半径为40![]() 的半圆形(以
的半圆形(以![]() 为圆心,
为圆心,![]() 为直径)绿化区域,现计划对其进行改建,在
为直径)绿化区域,现计划对其进行改建,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,在半圆上选定一点
,在半圆上选定一点![]() ,改建后的绿化区域由扇形区域
,改建后的绿化区域由扇形区域![]() 和三角形区域
和三角形区域![]() 组成,其面积为
组成,其面积为![]() ,设
,设![]()
(1)写出![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并指出
,并指出![]() 的取值范围;
的取值范围;
(2)试问![]() 多大时,改建后的绿化区域面积
多大时,改建后的绿化区域面积![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:数列![]() 对一切正整数
对一切正整数![]() 均满足
均满足![]() ,称数列
,称数列![]() 为“凸数列”,以下关于“凸数列”的说法:
为“凸数列”,以下关于“凸数列”的说法:
①等差数列![]() 一定是凸数列;
一定是凸数列;
②首项![]() ,公比
,公比![]() 且
且![]() 的等比数列
的等比数列![]() 一定是凸数列;
一定是凸数列;
③若数列![]() 为凸数列,则数列
为凸数列,则数列![]() 是单调递增数列;
是单调递增数列;
④若数列![]() 为凸数列,则下标成等差数列的项构成的子数列也为凸数列.
为凸数列,则下标成等差数列的项构成的子数列也为凸数列.
其中正确说法的序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬民族古典文化,学校举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确给改选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() 的概率;
的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于空间直角坐标系![]() 中的一点
中的一点![]() ,有下列说法:
,有下列说法:
①点![]() 到坐标原点的距离为
到坐标原点的距离为![]() ;
;
②![]() 的中点坐标为
的中点坐标为![]() ;
;
③点![]() 关于
关于![]() 轴对称的点的坐标为
轴对称的点的坐标为![]() ;
;
④点![]() 关于坐标原点对称的点的坐标为
关于坐标原点对称的点的坐标为![]() ;
;
⑤点![]() 关于坐标平面
关于坐标平面![]() 对称的点的坐标为
对称的点的坐标为![]() .
.
其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com