
����Ŀ����֪��H��x0 �� y0����ԲC��x2+y2+Dx+Ey+F=0�����е�CΪԲ�ģ�D2+E2��4F��0���⣬�ɵ�H��ԲC�����ߣ�����һ���е�ΪM��
��֤��|HM|= ![]() ��
��
��1����֪��H��x0 �� y0����ԲC��x2+y2+Dx+Ey+F=0�����е�CΪԲ�ģ�D2+E2��4F��0���⣬�ɵ�H��ԲC�����ߣ�����һ���е�ΪM��
��֤��|HM|= ![]() ��
��
��2����ͼ��P��ֱ��x=4��һ���㣬��PΪԲ�ĵ�ԲP������B��1��0����ֱ��l��ԲP�ڵ�B�������ߣ���A����1��0����ԲP���������߷ֱ���l����E��F���㣮
��֤��|EA|+|EB|Ϊ��ֵ��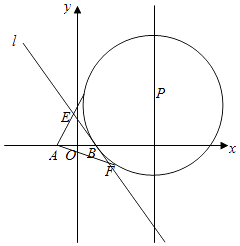
���𰸡�
��1��֤����ԲC�ķ���x2+y2+Dx+Ey+F=0��
��Ϊ������Ϊ ![]() +
+ ![]() =
= ![]() ��
��
C���� ![]() ����
���� ![]() ����ԲC�İ뾶Ϊr=
����ԲC�İ뾶Ϊr= ![]() ��
��
��ƽ�漸��֪ʶ��֪���ڡ�HMC�У���HMC=90�㣻
��HM2=HC2��CM2
= ![]() +
+ ![]() ��
�� ![]()
= ![]() +
+ ![]() +Dx0+Ey0+F��
+Dx0+Ey0+F��
��|HM|= ![]()
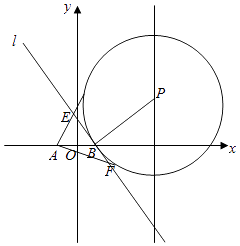
��2���⣺��ͼ��ʾ�����A����1��0����ԲP���������ߵ��е�ֱ�ΪM��N��
������֪EB=EM��
��EA+EB=|AM|��
��P������Ϊ��4��y0������ԲP�ķ���Ϊ
��x��4��2+��y��y0��2=9+y02��
��x2+y2��8x��2y0y+7=0��
�ɵڣ����ʵĽ��ۿ�֪
|AM|= ![]() =4��
=4��
��|EA|+|EB|=4��
��������1��������ɵ���RT��HMC��,���ݹ��ɶ����� �ý����
2���ɹ�һ����Բ���������ߵ����ʿɵ�EB=EM���ɵ�Ҫ��Ľ��EA+EB=|AM|�ٸ��ݣ�1���Ľ��ۿ���á�
�����㾫����������Ҫ������ֱ����Բ������λ�ù�ϵ�����֪ʶ�㣬��Ҫ����ֱ����Բ������λ�ù�ϵ��������Ϊ���룻������������Ϊ�ཻ,����ֱ�߽���Բ�ĸ��ߣ�Բ��ֱ����Ψһ������Ϊ���У�����ֱ�߽���Բ�����ߣ����Ψһ�Ĺ���������е������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ��������һ������������Ϊ������״������2.5�ף���ǰ��ǽ��2.5�ߵIJ�ɫ�ְ壬������2.5�ߵĸ��ϸְ壬���ְָ�ļ۸��ó��������㣨�����ְ�ĸ߾�Ϊ2.5�ף��øְ�ij��ȳ��Ե��۾������ְ�ļ۸�ÿ���ۣ���ɫ�ְ�Ϊ450Ԫ�����ϸְ�Ϊ200Ԫ���������������Ͻ��죬ÿƽ���ײ��Ϸ�Ϊ200Ԫ��ÿ�����Ϸѿ�����32000Ԫ���ڣ�
��1���跿ǰ��ǽ�ij�Ϊx������ǽ�ij�Ϊy�����ò��Ϸ�Ϊp������x��y��ʾp��
��2���ڲ��ϷѵĿ����¼������S�����ֵ�Ƕ��٣���ָ��ǰ��ǽ�ij���xӦΪ������ʱS���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax3+bx2��3x��x=��1��ȡ�ü�ֵ
��1������f��x���Ľ���ʽ��
��2����֤����������[��1��1]�����������Ա�����ֵx1 �� x2 �� ����|f��x1����f��x2��|��4��
��3��������A��1��m����m�٩�2����������y=f��x�����������ߣ���ʵ��m�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=lnx+ ![]() x2 ��
x2 ��
��1��������f��x����x=1�������߷��̣�
��2����PΪ����f��x���ϵĵ㣬������C�ڵ�P�����ߵ�б�ʵ���Сֵ����б�Ǧ���ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC���ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c��acosB=4��bsinA=3��
��1����tanB���߳�a��ֵ��
��2������ABC�����S=9�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() ��
�� ![]() ��
�� ![]() ����|
����| ![]() |=2��|
|=2��| ![]() +
+ ![]() |=6��|
|=6��| ![]() |=|
|=| ![]() |����
|���� ![]() ��
�� ![]() ����|
����| ![]() ��
�� ![]() |��ȡֵ��ΧΪ�� ��
|��ȡֵ��ΧΪ�� ��
A.[4��8]
B.[4 ![]() ��8
��8 ![]() ]
]
C.��4��8��
D.��4 ![]() ��8
��8 ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪2sinA��cosB=2sinBcosC���ҽ�BΪ�۽ǣ�
��1�����C�Ĵ�С��
��2����a=2��b2+c2��a2= ![]() bc�����ABC�������
bc�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������ABCD-A1B1C1D1��,��M��A1D1���е�,��N��CD���е�,�÷�֤��֤��ֱ��BM��ֱ��A1N����������ֱ��.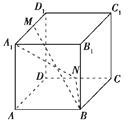
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=x3+3ax2+bx+a2��a��1����x=��1ʱ�ļ�ֵΪ0������a��b��ֵ����f��x���ĵ������䣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com