
【题目】设点![]() ,满足|PA|=2|PB|的点
,满足|PA|=2|PB|的点![]() 的轨迹是圆M:x2+y2
的轨迹是圆M:x2+y2![]() x+Ey+F=0.直线AB与圆M相交于C,D两点,
x+Ey+F=0.直线AB与圆M相交于C,D两点,![]() ,且点C的纵坐标为
,且点C的纵坐标为![]() .
.
(1)求a,b的值;
(2)已知直线l:x+y+2=0与圆M相交于G,H两点,求|GH|.
【答案】(1)a=3,b=2;(2)![]() .
.
【解析】
(1)把关系式|PA|=2|PB|用坐标表示出来得轨迹方程与已知方程比较可得![]() ,设点
,设点![]() ,由
,由![]() 可求得
可求得![]() ,这样得出圆
,这样得出圆![]() 的方程.
的方程.
(2)求出圆心到直线的距离![]() ,由垂径定理可求得弦长.
,由垂径定理可求得弦长.
(1)∵点A(a,1),B(﹣1,b),点P(x,y)且满足|PA|=2|PB|,
∴![]() ,
,
整理得:x2![]() ,
,
又∵点P(x,y)的轨迹是圆M:x2+y2![]() x+Ey+F=0,
x+Ey+F=0,
∴![]() ,解得a=3,
,解得a=3,
设点C(x0,![]() ),
),
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,解得b=2;
,解得b=2;
(2)由(1)圆M的方程为:x2+y2![]() x
x![]() y
y![]() 0,
0,
化为标准方程得:(x![]() )2+(y
)2+(y![]() )2
)2![]() ,圆心M(
,圆心M(![]() ,
,![]() ),半径r
),半径r![]() ,
,
∴圆心M到直线l:x+y+2=0的距离![]()
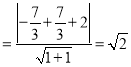 ,
,
∴|GH|=2![]() 2
2![]() .
.


科目:高中数学 来源: 题型:
【题目】今年入冬以来,我市天气反复.在下图中统计了我市上个月前15天的气温,以及相对去年同期的气温差(今年气温-去年气温,单位:摄氏度),以下判断错误的是( )
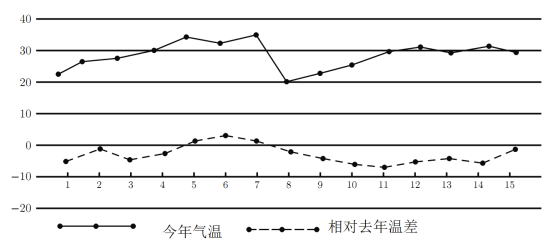
A.今年每天气温都比去年气温低B.今年的气温的平均值比去年低
C.今年8-12号气温持续上升D.今年8号气温最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”(已知1丈为10尺)该锲体的三视图如图所示,则该锲体的体积为( )
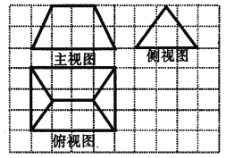
A. 12000立方尺B. 11000立方尺
C. 10000立方尺D. 9000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:若x2+y2>2,则|x|>1或|y|>1;命题q:直线mx-2y-m-2=0与圆x2+y2-3x+3y+2=0必有两个不同交点,则下列说法正确的是( )
A. p为真命题 B. p∧(q)为真命题
C. (p)∨q为假命题 D. (p)∨(q)为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到其准线的距离为
的焦点到其准线的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,问抛物线
两点,问抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是正三角形?若存在,求出点
是正三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,某地区植被覆盖面积![]() 公顷
公顷![]() 与当地气温下降的度数
与当地气温下降的度数![]() 之间呈线性相关关系,对应数据如下:
之间呈线性相关关系,对应数据如下:
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
![]() 请用最小二乘法求出y关于x的线性回归方程;
请用最小二乘法求出y关于x的线性回归方程;
![]() 根据
根据![]() 中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少
中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少![]() ?
?
参考公式:线性回归方程![]() ;其中
;其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点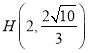 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)点![]() 在圆
在圆![]() 上,且
上,且![]() 在第一象限,过
在第一象限,过![]() 作
作![]() 的切线交椭圆于
的切线交椭圆于![]() 两点,问:
两点,问: ![]() 的周长是否为定值?若是,求出定值;若不是,说明理由.
的周长是否为定值?若是,求出定值;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com