
 如图,在菱形ABCD中,∠BAD=60°,AB=2$\sqrt{3}$,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P-BCD的外接球的表面积为( )
如图,在菱形ABCD中,∠BAD=60°,AB=2$\sqrt{3}$,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P-BCD的外接球的表面积为( )| A. | 28π | B. | 32π | C. | 16π | D. | 12π |
分析 利用球的对称性可知∠OEC=60°,利用等边三角形的性质和勾股定理求出球的半径,即可求出三棱锥P-BCD的外接球的表面积.
解答 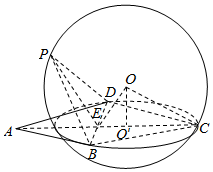 解:过球心O作OO′⊥平面BCD,则O′为等边三角形BCD的中心,
解:过球心O作OO′⊥平面BCD,则O′为等边三角形BCD的中心,
∵四边形ABCD是菱形,A=60°,
∴△BCD是等边三角形,
∵∠PEC=120°,∴∠OEC=60°;
∵AB=2$\sqrt{3}$,
∴CE=3,
∴EO′=1,CO′=2,
∴OO′=$\sqrt{3}$,
∴球的半径OC=$\sqrt{3+4}$=$\sqrt{7}$.
∴三棱锥P-BCD的外接球的表面积为4π•7=28π,
故选:A.
点评 本题考查了棱锥与外接球的关系,考查三棱锥P-BCD的外接球的表面积,找出∠OEC=60°是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
已知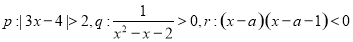 .
.
(1)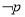 是
是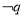 的什么条件?
的什么条件?
(2)若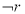 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个正方体削去一个角所几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),若削去的几何体中原正方体的顶点到截面的距离为h,削去的几何体中内切球的半径为R,则$\frac{h}{R}$的值为( )
一个正方体削去一个角所几何体的三视图如图所示(图中三个四边形都是边长为2的正方形),若削去的几何体中原正方体的顶点到截面的距离为h,削去的几何体中内切球的半径为R,则$\frac{h}{R}$的值为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | 2$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | $\frac{1+\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
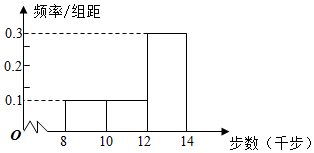 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com