
 如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )
如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{4}$ |
分析 要求cos∠DAO的值,由于A为一动点,故无法直接解三角形求出答案,我们可以构造与∠DAO相等的角,然后进行求解,过P点作x轴平行线,交圆弧于G,连接OG根据等腰三角形性质及垂径定理,结合同角或等角的余角相等,我们可以判断∠DAO=∠PGO,进而得到结论.
解答 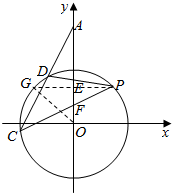 解:过P点作x轴平行线,交圆弧于G,连接OG.
解:过P点作x轴平行线,交圆弧于G,连接OG.
则:G点坐标为(-3,4),PG⊥EF,
∵PEF是以P为顶点的等腰三角形,
∴PG就是角DPC的平分线,
∴G就是圆弧CD的中点.
∴OG⊥CD,
∴∠DAO+∠GOA=90°.
而∠PGO+∠GOA=90°.
∴∠DAO=∠PGO
∴cos∠DAO=cos∠PGO=$\frac{3}{5}$.
故选B.
点评 本题考查的知识点是三角函数求值,其中利用等腰三角形性质及垂径定理,结合同角或等角的余角相等,构造与∠DAO相等的角∠PGO,是解答本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额( x)/千万元 | 3 | 5 | 6 | 7 | 9 |
| 利润额( y)/千万元 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在$\widehat{{A}{B}}$上且$\widehat{{A}{P}}=\frac{1}{3}\widehat{{A}{P}{B}}$,Q为PD上任意一点.
如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在$\widehat{{A}{B}}$上且$\widehat{{A}{P}}=\frac{1}{3}\widehat{{A}{P}{B}}$,Q为PD上任意一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com