
【题目】过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
, ![]() 两点,
两点, ![]() 为坐标原点,若
为坐标原点,若![]() ,则△
,则△![]() 的面积为( )
的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】【解法1】设∠AFx=θ(0<θ<π)及|BF|=m,∵|AF|=3,∴点A到准线l:x=-1的距离为3
∴2+3cosθ=3∴cosθ=![]() ,∵m=2+mcos(π-θ),∴
,∵m=2+mcos(π-θ),∴![]() ,
,
∴△AOB的面积为S=![]() ×
×![]() ×
×![]() ×sinθ=
×sinθ=![]() ×1×(3+
×1×(3+![]() )×
)×![]() =
=![]() .故选(C)
.故选(C)
【解法2】如图,设A![]()
![]() .易知抛物线y2=4x的焦点为F
.易知抛物线y2=4x的焦点为F![]() ,
,
准线为x=-1,故由抛物线的定义得![]() =x0-
=x0-![]() =3,解得x0=2,
=3,解得x0=2,
所以y0=-2![]() ,故A
,故A![]() .则直线AB斜率为k=
.则直线AB斜率为k=![]() =-2
=-2![]() ,
,
直线AB的方程为y=-2![]() x+2
x+2![]() ,联立
,联立![]()
消去y得2x2-5x+2=0,由x1x2=1,得A,B两点横坐标之积为1,所以点B的横坐标为![]() .
.
再由抛物线的定义得![]() =
=![]() -
-![]() =
=![]() ,
,![]() =
=![]() +
+![]() =3+
=3+![]() =
=![]() .
.
又因为点O到直线AB的距离为d=![]() ,所以S△AOB=
,所以S△AOB=![]() ×
×![]() ×
×![]() =
=![]() .故选(C)
.故选(C)


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
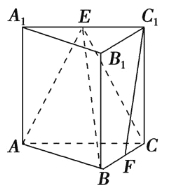
(1)求证:AB⊥平面B1BCC1; 平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为坐标原点,
为坐标原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是
A. 若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都没有公共点;
内的任意一条直线都没有公共点;
B. 若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都平行;
内的任意一条直线都平行;
C. 若直线![]() 上有无数个点不在平面
上有无数个点不在平面 ![]() 内,则
内,则![]() ;
;
D. 如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,生产1吨A种产品需要煤4吨、电18千瓦;生产1吨B种产品需要煤1吨、电15千瓦。现因条件限制,该企业仅有煤10吨,并且供电局只能供电66千瓦,若生产1吨A种产品的利润为10000元;生产1吨B种产品的利润是5000元,试问该企业如何安排生产,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系,![]() 点的极坐标为
点的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为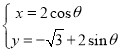 (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com