【题目】设函数
，若函数
恰有两个零点，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由题意得方程
有两个不同的实数根，从而得到函数
的图象和函数
的图象有两个不同的交点，画出两函数的图象，结合图象可得所求的范围．
∵函数
恰有两个零点，
∴方程有两个不同的实数根，即方程
有两个不同的实数根，
∴函数的图象和函数的图象有两个不同的交点．
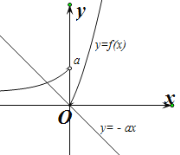
①当
时，显然不符合题意．
②当
时，函数的图象为过原点且斜率小于0的直线．
画出两函数的图象，如下图所示．
由图象可得两函数的图象总有两个不同的交点．
所以符合题意．
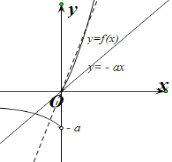
③当
时，函数的图象为过原点且斜率大于0的直线．
画出两函数的图象，如下图所示．
由图象可得，当
时，两函数的图象总有一个交点，
所以要使得两函数的图象再有一个交点，只需直线的斜率小于曲线在原点处的切线的斜率．
由
，得
，
所以
，
所以
，解得
，
所以
．
综上可得或．
故选A．
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案科目：高中数学 来源： 题型：
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关，通过随机调查200名高中生是否爱好某项运动，利用
列联表，由计算可得
，参照下表：
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是（ ）
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别无关”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司生产一种产品，从流水线上随机抽取100件产品，统计其质量指数并绘制频率分布直方图（如图1）：
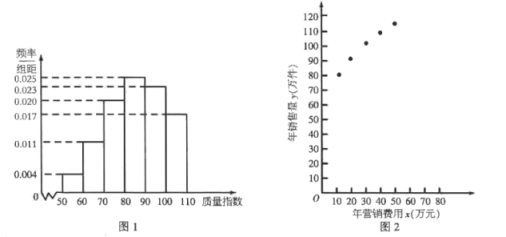
产品的质量指数在
的为三等品，在
的为二等品，在
的为一等品，该产品的三、二、一等品的销售利润分别为每件1.5，3.5,5.5（单位：元），以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
（1）求每件产品的平均销售利润；
（2）该公司为了解年营销费用
（单位：万元）对年销售量
（单位：万件）的影响，对近5年的年营销费用
和年销售量
数据做了初步处理，得到的散点图（如图2）及一些统计量的值.
|
|
|
|
16.30 | 24.87 | 0.41 | 1.64 |
表中
，
，
，
根据散点图判断，
可以作为年销售量（万件）关于年营销费用（万元）的回归方程.
（ⅰ）建立关于的回归方程；
（ⅱ）用所求的回归方程估计该公司应投入多少营销费，才能使得该产品一年的收益达到最大？（收益=销售利润-营销费用，取
）
参考公式：对于一组数据：
，
，
，
，其回归直线
的斜率和截距的最小乘估计分别为
，
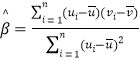查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在边长为60 cm的正方形铁片的四角上切去相等的正方形，再把它沿虚线折起，做成一个无盖的长方体箱子，箱底的边长是多少时，箱子的容积最大？最大容积是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝|3x＋2|.
(1)解不等式f(x)<4－|x－1|；
(2)已知m＋n＝1(m，n>0)，若|x－a|－f(x)≤
(a>0)恒成立，求实数a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图①，已知矩形ABCD满足AB=5，
，沿平行于AD的线段EF向上翻折（点E在线段AB上运动，点F在线段CD上运动），得到如图②所示的三棱柱
.
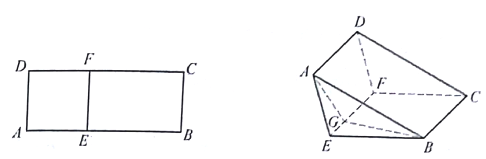
⑴若图②中△ABG是直角三角形，这里G是线段EF上的点，试求线段EG的长度x的取值范围；
⑵若⑴中EG的长度为取值范围内的最大整数，且线段AB的长度取得最小值，求二面角
的值；
⑶在⑴与⑵的条件都满足的情况下，求三棱锥A-BFG的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知偶函数
满足
，现给出下列命题：①函数是以2为周期的周期函数；②函数是以4为周期的周期函数；③函数
为奇函数；④函数
为偶函数，则其中真命题的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
