
【题目】已知函数![]() ;
;
(1)若![]() ,求证:
,求证: ![]() 在
在![]() 上单调递增;
上单调递增;
(2)若![]() ,试讨论
,试讨论![]() 零点的个数.
零点的个数.
【答案】(1)见解析(2)当![]() 时,
时, ![]() 没有零点;
没有零点; ![]() 时,
时, ![]() 有一个零点;
有一个零点; ![]() 时,
时, ![]() 有两个零点.
有两个零点.
【解析】试题分析:(1)![]() 时,
时, ![]() ,
, ![]() ,要证
,要证![]() 在
在![]() 上单调递增,只要证:
上单调递增,只要证: ![]() 对
对![]() 恒成立,只需证明
恒成立,只需证明![]() (当且仅当
(当且仅当![]() 时取等号).
时取等号).![]() (当且仅当
(当且仅当![]() 时取等号),即可证明
时取等号),即可证明![]() ;
;
(2)求函数的导数,根据函数极值和导数的关系,分![]()
![]() 讨论,即可判断函数
讨论,即可判断函数![]() 零点的个数.
零点的个数.
试题解析:(1)![]() 时,
时, ![]() ,
, ![]() ,
,
要证![]() 在
在![]() 上单调递增,只要证:
上单调递增,只要证: ![]() 对
对![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() (当且仅当
(当且仅当![]() 时等号成立),
时等号成立),
令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,故
,故![]() 在(0,1)上单调递减,在
在(0,1)上单调递减,在![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
![]()
![]() (当且仅当
(当且仅当![]() 时等号成立)
时等号成立)
![]() 在
在![]() 上单调递增.
上单调递增.
(2)由![]() 有
有![]() ,显然
,显然![]() 是增函数,
是增函数,
令![]() ,得
,得![]() ,
, ![]() ,
, ![]() ,
,
则![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴![]() 有极小值,
有极小值, ![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 有一个零点1;
有一个零点1;
②![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 没有零点;
没有零点;
③当![]() 时,
时, ![]() ,
, ![]() ,又
,又![]() ,
,
又对于函数![]() ,
, ![]() 时
时![]() ,
,
∴当![]() 时,
时, ![]() ,即
,即![]() ,
,
∴![]()
![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() ,
, ![]() ,∴
,∴![]() 有两个零点,
有两个零点,
综上,当![]() 时,
时, ![]() 没有零点;
没有零点; ![]() 时,
时, ![]() 有一个零点;
有一个零点; ![]() 时,
时, ![]() 有两个零点.
有两个零点.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】设正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若正项等比数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意
,若对任意![]() ,均有
,均有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有如下命题:
有如下命题:
①![]() ; ②函数的图象关于原点中心对称;
; ②函数的图象关于原点中心对称;
③函数的定义域与值域相同; ④函数的图象必经过第二、四象限.
其中正确命题的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年是某市大力推进居民生活垃圾分类的关键一年,有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识”的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图所示:
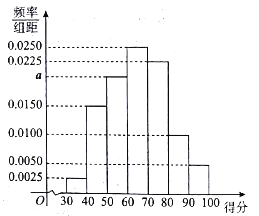
(1)估计该组数据的中位数、众数;
(2)由频率分布直方图可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
, ![]() 近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求
近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求![]() ;
;
(3)在(2)的条件下,有关部门为此次参加问卷调查的市民制定如下奖励方案:
(ⅰ)得分不低于![]() 可获赠2次随机话费,得分低于
可获赠2次随机话费,得分低于![]() 则只有1次;
则只有1次;
(ⅱ)每次赠送的随机话费和对应概率如下:

现有一位市民要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: ![]() ,
,
若![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,手机的功能逐渐强大,很大程度上代替了电脑、电视.为了了解某高校学生平均每天使用手机的时间是否与性别有关,某调查小组随机抽取了30名男生、20名女生进行为期一周的跟踪调查,调查结果如下表所示:
平均每天使用手机超过3小时 | 平均每天使用手机不超过3小时 | 合计 | |
男生 | 25 | 5 | 30 |
女生 | 9 | 11 | 20 |
合计 | 34 | 16 | 50 |
(1)能否在犯错误的概率不超过0.01的前提下认为学生使用手机的时间长短与性别有关?
(2)在这20名女生中,调查小组发现共有15人使用国产手机,在这15人中,平均每天使用手机不超过3小时的共有9人.从平均每天使用手机超过3小时的女生中任意选取3人,求这3人中使用非国产手机的人数X的分布列和数学期望.
参考公式: 
P(K2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ex+3x2-2x+1+b,x∈R的图象在x=0处的切线方程为y=ax+2.
(1)求函数f(x)的单调区间与极值;
(2)若存在实数x,使得f(x)-2x2-3x-2-2k≤0成立,求整数k的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过C(1,-1),D(-1,1)两点,且圆心M在x+y-2=0上.
(1)求圆M的方程;
(2)设点P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一研究性学习小组对春季昼夜温差大小与某大豆种子发芽多少之间的关系进行分析研究,他们分别记录了4月1日至4月5日的每天昼夜温差与实验室每天每100颗种子的发芽数,得到如下数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 8 | 12 | 13 | 11 | 10 |
发芽数 | 18 | 26 | 30 | 25 | 20 |
该学习组所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻2天的数据的概率;
(2)若选取的是4月1日与4月5日这2组数据做检验,请根据4月2日至4月4日这3组数据求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)所得的线性回归方程是否可靠?
参考公式和数据: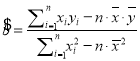 ,
,![]() ;
;![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com