
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为![]() ,点
,点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)已知点![]() ,是椭圆
,是椭圆![]() 上的两点.
上的两点.
(ⅰ)若![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的面积;
的面积;
(ⅱ)若![]() ,证明:
,证明: ![]() 不可能为等边三角形.
不可能为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,且
,且![]() ,设命题p:函数
,设命题p:函数![]() 在
在![]() 上单调递减;命题q:函数
上单调递减;命题q:函数![]() 在
在![]() 上为增函数,
上为增函数,
(1)若“p且q”为真,求实数c的取值范围
(2)若“p且q”为假,“p或q”为真,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF
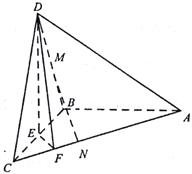
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 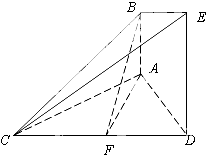
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com