
【题目】如图所示的矩形![]() 中,
中, ![]() ,点
,点![]() 为
为![]() 边上异于
边上异于![]() ,
, ![]() 两点的动点,且
两点的动点,且![]() ,
, ![]() 为线段
为线段![]() 的中点,现沿
的中点,现沿![]() 将四边形
将四边形![]() 折起,使得
折起,使得![]() 与
与![]() 的夹角为
的夹角为![]() ,连接
,连接![]() ,
, ![]() .
.

(1)探究:在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,说明点
,若存在,说明点![]() 的位置,若不存在,请说明理由;
的位置,若不存在,请说明理由;
(2)求三棱锥![]() 的体积的最大值,并计算此时
的体积的最大值,并计算此时![]() 的长度.
的长度.
【答案】(1)见解析.(2)见解析.
【解析】试题分析:(1) 取线段EF的中点M,易证GM∥DF ,从而得到GM∥平面BDF;(2) 因为CF∥DE,且AE与CF的夹角为60°,故AE与DE的夹角为60°,利用等体积法表示体积,进而得到体积的最大值,及此时DE的长度.
试题解析:
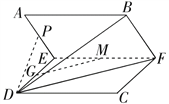
(1)如图所示,取线段EF的中点M,下证GM∥平面BDF;
因为G为线段ED中点,M为线段EF的中点,
故GM为△EDF的中位线,故GM∥DF,
又GM平面BDF,DF平面BDF,故GM∥平面BDF;
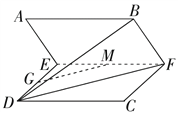
(2)因为CF∥DE,且AE与CF的夹角为60°,
故AE与DE的夹角为60°,
过D作DP垂直于AE交AE于P,
因为DE⊥EF,AE⊥EF,故DP为点D到平面ABFE的距离,
设DE=x,则AE=BF=4-x,
由①知GM∥DF,
故VG-BDF=VM-BDF=VD-MBF=![]() ·S△MBF·DP=
·S△MBF·DP=![]() ×
×![]() ×
×![]() x
x
=![]()
![]() ·x≤
·x≤![]() ,
,
当且仅当4-x=x时等号成立,此时x=DE=2,
故三棱锥G-BDF的体积最大值为![]() ,此时DE的长度为2.
,此时DE的长度为2.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上的两个点,点
上的两个点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .设抛物线
.设抛物线![]() 的焦点在直线
的焦点在直线![]() 的下方.
的下方.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且![]() ,过
,过![]() 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为![]() . 判断四边形
. 判断四边形![]() 是否为梯形,并说明理由.
是否为梯形,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切.
相切.
(1)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() ;
;
(2)设圆![]() 与
与![]() 轴的负半轴的交点为
轴的负半轴的交点为![]() ,过点
,过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,且
两点,且![]() ,试证明直线
,试证明直线![]() 恒过一定点,并求出该定点的坐标.
恒过一定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn.已知2Sn=3n+3.
(1)求{an}的通项公式;
(2)若数列{bn}满足anbn=log3an,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l的参数方程为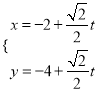 ,直线l与曲线C分别交于M,N两点.若|PM|,|MN|,|PN|成等比数列,则a的值为________.
,直线l与曲线C分别交于M,N两点.若|PM|,|MN|,|PN|成等比数列,则a的值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P—A1B1C1D1,下部的形状是正四棱柱ABCD—A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
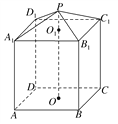
(1)若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为6 m,则当PO1为多少时,仓库的容积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com