
已知a=(1,2),b=(-2,n) (n>1),a与b的夹角是45°.
(1)求b;
(2)若c与b同向,且a与c-a垂直,求c.
(1) b=(-2,6) (2) (-1,3).
解析试题分析:(1)利用向量夹角公式可得关于n的方程,解出n即得向量b;
(2)由c与b同向,同向,可设c=λb (λ>0),利用向量垂直的充要条件可求得λ,代入即可求得c;
(1)a·b=2n-2,|a|=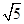 ,|b|=
,|b|=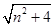 ,
,
∴cos 45°=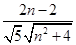 =
=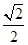 ,∴3n2-16n-12=0,∴n=6或n=-
,∴3n2-16n-12=0,∴n=6或n=-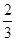 (舍),∴b=(-2,6).
(舍),∴b=(-2,6).
(2)由(1)知,a·b=10,|a|2=5.又c与b同向,故可设c=λb (λ>0),(c-a)·a=0,
∴λb·a-|a|2=0,∴λ= =
=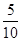 =
=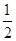 ,∴c=
,∴c=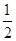 b=(-1,3).
b=(-1,3).
考点:平面向量数量积的运算;利用数量积判断两向量的垂直关系.


科目:高中数学 来源: 题型:解答题
已知中心在原点,对称轴为坐标轴的椭圆C的一个焦点在抛物线 的准线上,且椭圆C过点
的准线上,且椭圆C过点 .
.
(1)求椭圆C的方程;
(2)点A为椭圆C的右顶点,过点 作直线
作直线 与椭圆C相交于E,F两点,直线AE,AF与直线
与椭圆C相交于E,F两点,直线AE,AF与直线 分别交于不同的两点M,N,求
分别交于不同的两点M,N,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com