Question

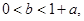设若关于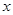的不等式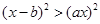的解集中的整数恰有3个，则（ ）

A．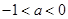

B．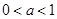

C．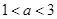

D．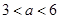

Answer 1

C

解析试题分析：要使关于x的不等式（x-b）²＞（ax）²的解集中的整数恰有3个，那么此不等式的解集不能是无限区间，从而其解集必为有限区间，由题得不等式（x-b）²＞（ax）²，即（a²-1）x²+2bx-b²＜0，它的解应在两根之间，，因此应有 a²-1＞0，解得a＞1或a＜-1，注意到0＜b＜1+a，从而a＞1，，故有△=4b²+4b²（a²-1）=4a²b²＞0，，不等式的解集为或者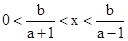
若不等式的解集为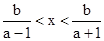又由0＜b＜1+a得0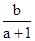＜＜1，
故-3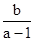＜＜-2，0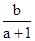＜＜1，这三个整数解必为-2，-1，0，2（a-1）＜b≤3 （a-1），，注意到a＞1，并结合已知条件0＜b＜1+a．，故要满足题设条件，只需要2（a-1）＜1+a＜3（a-1） 即可，则，b＞2a-2，b＜3a-3，又0＜b＜1+a，故 1+a＞2a-2，3a-3＞0解得1＜a＜3，综上1＜a＜3．故选C．
考点：本试题主要考查了解一元二次不等式解法，二次函数的有关知识，逻辑思维推理能力，含有两个变量的题目是难题．
点评：解决该试题的关键是对于二次不等式的开口方向和因式分解的正确处理。