
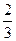 .(1)求连续射击5次,恰有3次击中目标的概率;
.(1)求连续射击5次,恰有3次击中目标的概率;科目:高中数学 来源:不详 题型:解答题
 用户推出了多款
用户推出了多款 应用,如“
应用,如“ 农场”、“
农场”、“ 音乐”、“
音乐”、“ 读书”等.某校研究性学习小组准备举行一次“
读书”等.某校研究性学习小组准备举行一次“ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:
使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:| 班级 | 一班 | 二班 | 三班 | 四班 |
| 人数 | 2人 | 3人 | 4人 | 1人 |
 农场、
农场、 音乐、
音乐、 读书中任意选择一项,他们选择
读书中任意选择一项,他们选择 农场的概率都为
农场的概率都为 ;选择
;选择 音乐的概率都为
音乐的概率都为 ;选择
;选择 读书的概率都为
读书的概率都为 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 读书的总人数为随机变量
读书的总人数为随机变量 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数. 的概率分布;
的概率分布;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
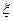 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求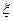 的分布列和数学期望
的分布列和数学期望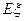 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.84,4.84 | B.84,1.6 | C.85,1.6 | D.85,4 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示取出的3张卡片的最大数字,求:
表示取出的3张卡片的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望; ,求
,求 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ξ∈N)~正态
ξ∈N)~正态 .3,估计该班学
.3,估计该班学
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com