
 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,
如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,分析 (1)利用平面与平面垂直的性质定理得出BC⊥平面PDC,即可证明BC⊥PD;
(2)利用等体积法,求点C到平面PDA的距离.
解答 (1)证明:因为四边形ABCD是长方形,所以BC⊥CD,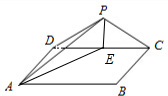
因为平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,BC?面ABCD,
所以BC⊥平面PDC,
因为PD?平面PDC,
所以BC⊥PD;
(2)解:取CD的中点E,连接AE和PE,
因为PD=PC,所以PE⊥CD,
在Rt△PED中,PE=$\sqrt{16-9}$=$\sqrt{7}$.
因为平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,PE?平面PDC,
所以PE⊥平面ABCD.
由(1)知:BC⊥平面PDC,
因为四边形ABCD是长方形,所以BC∥AD,
所以AD⊥平面PDC,
因为PD?平面PDC,所以AD⊥PD.
设点C到平面PDA的距离为h.
因为VC-PDA=VP-ACD,
所以h=$\frac{\frac{1}{2}×3×6×\sqrt{7}}{\frac{1}{2}×3×4}$=$\frac{3\sqrt{7}}{2}$,所以点C到平面PDA的距离是$\frac{3\sqrt{7}}{2}$.
点评 本题考查平面与平面垂直的性质,线面垂直与线线垂直的判定,考查三棱锥体积等知识,注意解题方法的积累,属于中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{15}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数 | [50,59) | [60,69) | [70,79) | [80,89) | [90,100) |
| 甲班频数 | 5 | 6 | 4 | 4 | 1 |
| 乙班频数 | 1 | 3 | 6 | 5 |
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
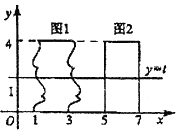 我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.
我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理y(分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{16}{65}$ | B. | $\frac{16}{65}$ | C. | -$\frac{56}{65}$ | D. | $\frac{56}{65}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com