【题目】三棱锥
的三视图如图所示，
.
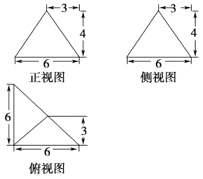
（1）求该三棱锥的表面积；
（2）求该三棱锥内切球的体积.
【答案】（1）
（2）
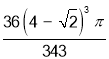
【解析】
（1）根据三视图可知，此三棱锥的底面是腰长为6的等腰直角三角形
，顶点
在底面上的摄影是底面直角三角形斜边的中点，且三棱锥的高为4，要求表面积，再利用三视图，明确
，
，
上的高即可.
（2）根据三棱锥的体积等于以球心为顶点，三棱锥的四个面为底的小三棱锥的体积之和求解.
（1）如图所示：
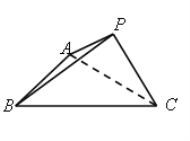
由三视图可知，此三棱锥的底面是腰长为6的等腰直角三角形 ，且
，顶点 在底面上的摄影是底面直角三角形斜边的中点，且三棱锥的高为4，
在
中，边上的高为5，
在
中，边上的高为5，
在
中，边上的高为4，
所以该三棱锥的表面积
（2）设内切球的球心为
，半径为
则由
得
解得
，
所以该三棱锥内切球的体积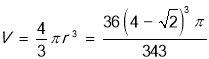
科目：高中数学 来源： 题型：
【题目】某亲子公园拟建议广告牌，将边长为
米的正方形ABCD和边长为1米的正方形AEFG在A点处焊接，AM、AN、GM、DN均用加强钢管支撑，其中支撑钢管GM、DN垂直于地面于M点和N点，且GM、DN、MN长度相等
不计焊接点大小
若
时，求焊接点A离地面距离；
若记
，求加强钢管AN最长为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】假设平面点集
具有性质：（1）任意三点不共线；（2）任意两点距离各不相等.对于中两点
、
，若存在点
使得
，则称
是的一条“中边”；对于中三点、、
，若、
、
都是的中边，则称
是的“中边三角形”.求最小的
，使得任意具有性质（1）和（2）的元平面点集中必存在中边三角形.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】越接近高考学生焦虑程度越强，四个高三学生中大约有一个有焦虑症，经有关机构调查，得出距离高考周数与焦虑程度对应的正常值变化情况如下表：
周数x | 6 | 5 | 4 | 3 | 2 | 1 |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
(1)作出散点图：
(2)根据上表数据用最小二乘法求出y关于x的线性回归方程 (精确到0.01)；
(3)根据经验，观测值为正常值的0.85～1.06为正常，若1.06～1.12为轻度焦虑，1.12～1.20为中度焦虑，1.20及其以上为重度焦虑，若为中度焦虑及其以上，则要进行心理疏导，若一个学生在距高考第二周时观测值为100，则该学生是否需要进行心理疏导？
（
, 
）
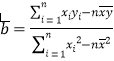查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在“数学发展史”知识测验后,甲、乙、丙三人对成绩进行预测:
甲说:我的成绩比乙高;
乙说:丙的成绩比我和甲的都高;
丙说:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人中预测正确的是________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(本小题满分15分)
在等差数列{an}中，a1=1，公差d≠0，且a1，a2，a5是等比数列{bn}的前三项．
(1)求数列{an}和{bn}的通项公式；
(2)设cn=an·bn，求数列{cn}的前n项和Sn．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个生产公司投资A生产线500万元，每万元可创造利润
万元，该公司通过引进先进技术，在生产线A投资减少了x万元，且每万元的利润提高了
；若将少用的x万元全部投入B生产线，每万元创造的利润为
万元，其中
．
若技术改进后A生产线的利润不低于原来A生产线的利润，求x的取值范围；
若生产线B的利润始终不高于技术改进后生产线A的利润，求a的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
