
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
分析 方程$f(x)-ax=\frac{5}{2}$有3个不同的解,即$f(x)=ax+\frac{5}{2}$有3个不同的解,等价于y=f(x)与$y=ax+\frac{5}{2}$的图象有3个不同的交点,因为直线$y=ax+\frac{5}{2}$恒过$({0,\;\;\frac{5}{2}})$,所以满足条件的直线应在图中的l1与l2之间,求出斜率,即可得出结论.
解答  解:f(x)的图象如图所示,方程$f(x)-ax=\frac{5}{2}$有3个不同的解,即$f(x)=ax+\frac{5}{2}$有3个不同的解,
解:f(x)的图象如图所示,方程$f(x)-ax=\frac{5}{2}$有3个不同的解,即$f(x)=ax+\frac{5}{2}$有3个不同的解,
等价于y=f(x)与$y=ax+\frac{5}{2}$的图象有3个不同的交点,
因为直线$y=ax+\frac{5}{2}$恒过$({0,\;\;\frac{5}{2}})$,
所以满足条件的直线应在图中的l1与l2之间,斜率分别是${k_1}=\frac{{\frac{5}{2}-1}}{0-1}=-\frac{3}{2}$,${k_2}=\frac{{\frac{5}{2}-0}}{0-1}=-\frac{5}{2}$,故$a∈({-\frac{5}{2},\;\;-\frac{3}{2}}]$,
故选B.
点评 本题考查方程解的研究,考查数形结合的数学思想,考查学生分析解决问题的能力,正确转化是关键.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G为BC的中点.
如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
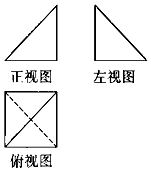 如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )
如图1,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的表面积是( )| A. | $2+4\sqrt{2}+2\sqrt{3}$ | B. | $2+4\sqrt{2}+\sqrt{6}$ | C. | $2+4\sqrt{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某中学高三年级有400名学生参加月考,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示.
某中学高三年级有400名学生参加月考,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数,且在区间$(0,\frac{π}{2})$上单调递增 | B. | 奇函数,且在区间$(0,\frac{π}{2})$上单调递减 | ||
| C. | 偶函数,且在区间$(0,\frac{π}{2})$上单调递增 | D. | 偶函数,且在区间$(0,\frac{π}{2})$上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com