
三次函数当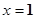 时有极大值
时有极大值 ,当
,当 时有极小值
时有极小值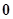 ,且函数过原点,则此函数是( )
,且函数过原点,则此函数是( )
A. B.
B.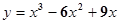
C.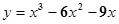 D.
D.
B
【解析】
试题分析:本题是据题意求参数的题,题目中x=1时有极大值4,当x=3时有极小值0,且函数图象过原点,可转化出五个等式,则其四建立方程.解:f’(x)=3a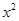 +2bx+c(a≠0),∵x=1时有极大值4,当x=3时有极小值0,∴f’(1)="3a+2b+c=0"
①f’(3)="27a+6b+c=0"
②f(1)="a+b+c+d=4"
③又函数图象过原点,所以 d="0" ④,①②③④联立得 a=1,b=-6,c=9,故函数f(x)=
+2bx+c(a≠0),∵x=1时有极大值4,当x=3时有极小值0,∴f’(1)="3a+2b+c=0"
①f’(3)="27a+6b+c=0"
②f(1)="a+b+c+d=4"
③又函数图象过原点,所以 d="0" ④,①②③④联立得 a=1,b=-6,c=9,故函数f(x)=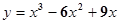 ,故选B.
,故选B.
考点:导数的运用
点评:本小题考点是导数的运用,考查导数与极值的关系,本题的特点是用导数一极值的关建立方程求参数---求函数的表达式


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com