
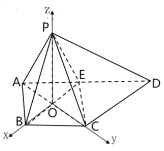
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,其中
为直角梯形,其中![]() ∥
∥![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 和
和![]() 交于点
交于点![]() ,且
,且![]() 平面
平面![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)见解析(2)![]()
【解析】
(1)由已知证明四边形![]() 是平行四边形,进一步证得四边形
是平行四边形,进一步证得四边形![]() 为正方形,得
为正方形,得![]() ,求解三角形证明
,求解三角形证明![]() ,由线面垂直的判定可得
,由线面垂直的判定可得![]() 平面
平面![]() ,得到
,得到![]() ,再由直线与平面垂直的判定可得
,再由直线与平面垂直的判定可得![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() ;
;
(2)由于![]() 两两垂直,故以
两两垂直,故以![]() 为原点,
为原点,![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,然后求出平面
,然后求出平面![]() 的法向量,再利用向量的夹角公式可求得结果.
的法向量,再利用向量的夹角公式可求得结果.
(1)因为![]() 是
是![]() 的中点,所以四边形
的中点,所以四边形![]() 是平行四边形,又因为
是平行四边形,又因为![]() ,所以四边形
,所以四边形![]() 是正方形,所以
是正方形,所以![]() ;
;
又因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,故
,故![]()
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ;
;
又因为![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由(1)知![]() 两两垂直,故以
两两垂直,故以![]() 为原点,
为原点,![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,
,
由(1)知四棱锥![]() 为正四棱锥,故
为正四棱锥,故![]() ,所以
,所以![]() 为等腰直角三角形,故
为等腰直角三角形,故![]() ,则
,则![]() ,
,
所以![]()
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,得
,得
 ,即
,即![]() ,令
,令![]() ,则
,则![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
那么 ,
,
因为![]() ,所以
,所以![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角
所成角![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点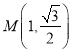 ,
,![]() 的参数方程为
的参数方程为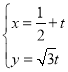 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·湖南师大附中摸底)已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,则直线l的方程是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)平面![]() 平面
平面![]()
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的曲线图是2020年1月25日至2020年2月12日陕西省及西安市新冠肺炎累计确诊病例的曲线图,则下列判断正确的是( )
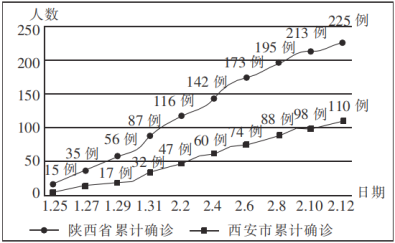
A.1月31日陕西省新冠肺炎累计确诊病例中西安市占比超过了![]()
B.1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势
C.2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了97例
D.2月8日到2月10日西安市新冠肺炎累计确诊病例的增长率大于2月6日到2月8日的增长率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com