
 如图,有一正方形钢板ABCD缺损一角(图中的阴影部分),边缘线OC是以直线AD为对称轴,以线段AD的中点O为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线EF,可使剩余的直角梯形的面积最大?并求其最大值.
如图,有一正方形钢板ABCD缺损一角(图中的阴影部分),边缘线OC是以直线AD为对称轴,以线段AD的中点O为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线EF,可使剩余的直角梯形的面积最大?并求其最大值. | 1 |
| 4 |
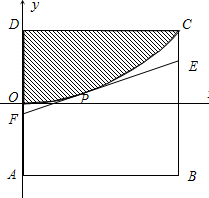 解:以O为原点,直线AD为y轴,建立如图所示的直角坐标系,依题意可设抛物线弧OC的方程为y=ax2(0≤x≤2)
解:以O为原点,直线AD为y轴,建立如图所示的直角坐标系,依题意可设抛物线弧OC的方程为y=ax2(0≤x≤2)| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |


科目:高中数学 来源:2011-2012学年福建省莆田市仙游一中高二(下)期末数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年广东省深圳市高考数学一模试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010-2011学年深圳市高三第一次调研考试数学文卷 题型:解答题
(本题满分12分)
如图,有一正方形钢板 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线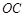 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段 的中点
的中点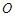 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线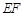 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年深圳市高三第一次调研考试数学文卷 题型:解答题
(本题满分12分)
如图,有一正方形钢板 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线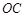 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段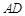 的中点
的中点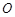 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com