
【题目】已知命题P:函数 ![]() 的定义域为R;命题q:x∈R,使不等式a>e2x﹣ex成立;命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
的定义域为R;命题q:x∈R,使不等式a>e2x﹣ex成立;命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
【答案】解:若命题p为真命题,则 ![]() 在x∈R恒成立,
在x∈R恒成立,
当a=0时显然不成立,
当a≠0时, ![]() ;
;
若命题q为真命题,则 ![]() ,
,
由命题“p∨q”为真命题,“p∧q”为假命题知p,q一真一假,
若p真q假,则 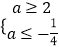 ,无解,
,无解,
若p假q真,则 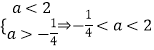 ,
,
综上所述, ![]()
【解析】分别求出p,q为真时的a的范围,再通过讨论p,q的真假,得到关于a的不等式组,解出即可.
【考点精析】解答此题的关键在于理解复合命题的真假的相关知识,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


科目:高中数学 来源: 题型:
【题目】
(1)解方程:25x+1﹣95x+2+500=0;
(2)已知关于x的不等式ax2﹣5x+b>0的解集为 ![]() ,求关于x的不等式ax2+5x+b<0的解集.
,求关于x的不等式ax2+5x+b<0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[2,4],x2﹣2x﹣2a≤0恒成立,命题q:f(x)=x2﹣ax+1在区间 ![]() 上是增函数.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
上是增函数.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(2a﹣1)x﹣lnx,a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线经过点(2,11),求实数a的值;
(2)若函数f(x)在区间(2,3)上单调,求实数a的取值范围;
(3)设 ![]() ,若对x1∈(0,+∞),x2∈[0,π],使得f(x1)+g(x2)≥2成立,求整数a的最小值.
,若对x1∈(0,+∞),x2∈[0,π],使得f(x1)+g(x2)≥2成立,求整数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某位股民购进某只股票,在接下来的交易时间内,他的这只股票先经历了 ![]() 次涨停(每次上涨
次涨停(每次上涨 ![]() ),又经历了
),又经历了 ![]() 次跌停(每次下跌
次跌停(每次下跌 ![]() ),则该股民这只股票的盈亏情况(不考虑其他费用)是( )
),则该股民这只股票的盈亏情况(不考虑其他费用)是( )
A.略有盈利
B.略有亏损
C.没有盈利也没有亏损
D.无法判断盈亏情况
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列各式: C ![]() =40;
=40;
C ![]() +C
+C ![]() =41;
=41;
C ![]() +C
+C ![]() +C
+C ![]() =42;
=42;
C ![]() +C
+C ![]() +C
+C ![]() +C
+C ![]() =43;
=43;
…
照此规律,当n∈N*时,
C ![]() +C
+C ![]() +C
+C ![]() +…+C
+…+C ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究男女同学空间想象能力的差异,孙老师从高一年级随机选取了20名男生、20名女生,进行空间图形识别测试,得到成绩茎叶图如下,假定成绩大于等于80分的同学为“空间想象能力突出”,低于80分的同学为“空间想象能力正常”. 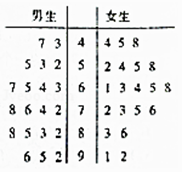
(1)完成下面2×2列联表,
空间想象能力突出 | 空间想象能力正常 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(2)判断是否有90%的把握认为“空间想象能力突出”与性别有关;
(3)从“空间想象能力突出”的同学中随机选取男生2名、女生2名,记其中成绩超过90分的人数为ξ,求随机变量ξ的分布列和数学期望. 下面公式及临界值表仅供参考: ![]()
P(X2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosωxsin(ωx+ ![]() )+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
)+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com