
【题目】已知集合A={x|y= ![]() },集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
},集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
(1)求A∩B;
(2)若A∪C=A,求实数m的取值范围.
科目:高中数学 来源: 题型:
【题目】如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=2 ![]() ,如图2.
,如图2. 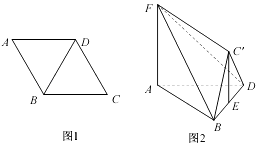
(1)求证:FA∥平面BC'D;
(2)求平面ABD与平面FBC'所成角的余弦值;
(3)在线段AD上是否存在一点M,使得C'M⊥平面FBC?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的奇函数y=f(x),满足对任意t∈R都有f(t)=f(1﹣t),且x ![]() 时,f(x)=﹣x2 , 则f(3)+f(﹣
时,f(x)=﹣x2 , 则f(3)+f(﹣ ![]() 的值等于( )
的值等于( )
A.﹣ ![]()
B.﹣ ![]()
C.﹣ ![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学巨著,内容极为丰富,其中卷六《均输》里有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”(“钱”是古代的一种重量单位),则其中第二人分得的钱数是( )
A.![]()
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2(a∈R).
(1)若g(x)= ![]() 有三个极值点x1 , x2 , x,求a的取值范围;
有三个极值点x1 , x2 , x,求a的取值范围;
(2)若f(x)≥﹣ax3+1对任意x∈[0,1]都恒成立的a的最大值为μ,证明:5 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2的图象经过点M(1,4),且在x=﹣2取得极值.
( I)求实数a,b的值;
( II)若函数f(x)在区间(m,m+1)上不单调,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过椭圆C: ![]() 的左顶点A作直线l,与椭圆C和y轴正半轴分别交于点P,Q.
的左顶点A作直线l,与椭圆C和y轴正半轴分别交于点P,Q.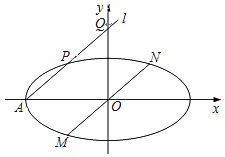
(1)若AP=PQ,求直线l的斜率;
(2)过原点O作直线l的平行线,与椭圆C交于点M,N,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com