练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在某校高三学生的数学校本课程选课过程中，规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙，情况如下表：
     
    		科目甲
    		科目乙
    		总计
    第一小组
    		1
    		5
    		6
    第二小组
    		2
    		4
    		6
    总计
    		3
    		9
    		12
    现从第一小组、第二小 组中各任选2人分析选课情况.
    （1）求选出的4 人均选科目乙的概率；
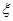    （2）设为选出的4个人中选科目甲的人数，求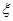的分布列和数学期望．
    （1）（2）的分布列为


    		 







    的数学期望 

    试题分析：（1）设“从第一小组选出的2人选科目乙”为事件，
    “从第二小组选出的2人选科目乙””为事件.由于事 件、相互独立，
    且,   .  4分
    所以选出的4人均选科目乙的概率为
       6分
    （2）设可能的取值为0,1,2,3.得
    ,  ,，
    … 9分
    的分布列为


    		 







    ∴的数学期望        12分
    点评：本题考查了随机事件的概率及随机变量的分布列、期望的综合运用，考查了学生的计算能力及解决实际问题的能力，掌握求分布列的步骤及期望公式是解决此类问题的关键
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取各10件样品，测量产品中某种元素的含量（单位：毫克）.如图是测量数据的茎叶图：

    规定：当产品中的此种元素含量不小于18毫克时，该产品为优等品.
    （1）试用上述样本数据估计甲、乙两厂生产的优等品率；
    （2）从乙厂抽出的上述10件样品中，随机抽取3件，求抽到的3件样品中优等品数的分布列及其数学期望；
    （3）从甲厂的10件样品中有放回的随机抽取3件，也从乙厂的10件样品中有放回的随机抽取3件，求抽到的优等品数甲厂恰比乙厂多2件的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分12分)
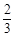    已知一种名贵花卉种子的发芽率为，现种植这种种子4粒，求：
    （Ⅰ）至少有3粒发芽的概率；
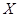    （Ⅱ）种子发芽的粒数的分布列及平均数.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    气象部门提供了某地区今年六月份(30天)的日最高气温的统计表如下：
    日最高气温t(单位：℃)
    		t≤22
    		22＜t≤28
    		28＜t≤32
    		t＞32
    天数
    		6
    		12
    		Y
    		Z
    由于工作疏忽，统计表被墨水污染，Y和Z数据不清楚，但气象部门提供的资料显示，六月份的日最高气温不高于32℃的频率为0.9.
    某水果商根据多年的销售经验，六月份的日最高气温t(单位：℃)对西瓜的销售影响如下表：
    日最高气温t(单位：℃)
    		t≤22
    		22＜t≤28
    		28＜t≤32
    		t＞32
    日销售额X(单位：千元)
    		2
    		5
    		6
    		8
    (1)求Y，Z的值；
    (2)若视频率为概率，求六月份西瓜日销售额的期望和方差；
    (3)在日最高气温不高于32℃时，求日销售额不低于5千元的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    样本中共有5个个体，其值分别为.若该样本的平均值为1，则样本方差为
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    篮球运动员在比赛中每次罚球命中得1分，罚不中得0分，已知某运动员罚球命中的概率为0.7，则他罚球2次（每次罚球结果互不影响）的得分的数学期望是       ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

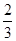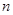    某人上楼梯，每步上一阶的概率为，每步上二阶的概率为，设该人从台阶下的平台开始出发，到达第阶的概率为.
    (1)求；;
    (2)该人共走了5步，求该人这5步共上的阶数ξ的数学期望.

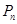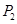    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

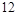    (本题满分12分)一厂家向用户提供的一箱产品共件，其中有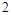件次品，用户先对产品进行抽检以决定是否接收．抽检规则是这样的：一次取一件产品检查（取出的产品不放回箱子），若前三次没有抽查到次品，则用户接收这箱产品；若前三次中一抽查到次品就立即停止抽检，并且用户拒绝接收这箱产品.
    （Ⅰ）求这箱产品被用户接收的概率；
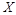    （Ⅱ）记抽检的产品件数为，求随机变量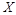的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    盒中有6只灯泡，其中2只次品，4只正品，有放回地从中任取两次，每次取一只，试求下列事件的概率：(1)取到的2只都是次品；(2)取到的2只中正品、次品各一只；
    (3)取到的2只中至少有一只正品.

    查看答案和解析>>

    同步练习册答案