分析:(I)设椭圆方程为
+=1(a>b>0),半焦距为c,由题意能够导出a=2,b=
,c=1,故椭圆方程为
+=1.
(II)设所求l'的方程为y=k(x+4),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量垂直的公式即可求得k值,从而解决问题.
解答: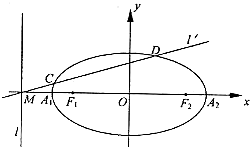
解:(I)设椭圆的方程为
+=1(a>b>0),半焦距为c
| | 则||=-a,||=a-c. | | 由题意,得 | | ∴a=2,b=,c=1 | | 故所求椭圆方程为+=1 |
| |
(II)点M的坐标为M(-4,0),设C、D两点坐标分别为C(x
1,y
1),D(x
2,y
2),l'的方程为y=k(x+4),代入椭圆方程整理,得
| | (3+4k2)x2+32k2x+64k2-12=0 | | 则x1+x2=-,x1x2= | | 由•=0得x1x2+y1y2=0 | | 又y1y2=k2[x1x2+4(x1+x2)+16] |
| |
后三个式子得
(1+k2)+4k2+16k2=0解得
k2=,代入第一个中检验有△>0,∴
k=±,
所以所求直线l’的主程为
y=±(x+4) 点评:本小题主要考查椭圆的标准方程、直线方程的应用、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查数形结合思想、方程思想.属于基础题.

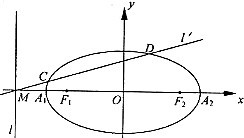 已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,
已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M, 解:(I)设椭圆的方程为
解:(I)设椭圆的方程为

 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.